2 MathML の基礎
概要: 数学用マークアップ言語 (MathML) バージョン 2.0
前: 1 導入
次: 3 プレゼンテーション・マークアップ
2 MathML の基礎
2.1 MathML 概論
2.1.1 MathML 要素の分類
2.1.2 プレゼンテーション・マークアップ
2.1.3 コンテンツ・マークアップ
2.1.4 マークアップの混在
2.2 文書中における MathML
2.3 MathML の例
2.3.1 プレゼンテーション・マークアップの例
2.3.2 コンテンツ・マークアップの例
2.3.3 混在したマークアップの例
2.4 MathML の構文と文法
2.4.1 MathML 構文と文法
2.4.2 XML 構文入門
2.4.3 子と引数
2.4.4 MathML の属性値
2.4.5 すべての MathML 要素に共通な属性
2.4.6 省略される空白の処理
2.1 MathML 概論
この章では、MathML の基本的な考え方を紹介します。
最初のセクションでは、MathML の全般的な設計について述べています。
続くセクションでは、この仕様書の残りの章を読む上で具体的に参照できるものとして、動機付けとなる例を多数掲載しています。
最後のセクションでは、MathML のすべてのマークアップに共通する構文と文法の基本的な特徴について述べています。
特に、セクション 2.4「MathML の構文と文法」 は、第 3 章「プレゼンテーション・マークアップ」、第 4 章「コンテンツ・マークアップ」 そして 第 5 章「Combining Presentation and Content Markup」の前に読むべきです。
This chapter introduces the basic ideas of MathML. The first section
describes the overall design of MathML. The second section presents a
number of motivating examples, to give the reader something concrete to
refer to while reading subsequent chapters of the MathML specification.
The final section describes basic features of the MathML syntax and
grammar, which apply to all MathML markup. In particular, Section 2.4 [MathML Syntax and Grammar] should be read before Chapter 3 [Presentation Markup], Chapter 4 [Content Markup] and Chapter 5 [Combining Presentation and Content Markup].
ウェブにおける数学のためのマークアップ言語を定義する上でまず直面する困難は、数学の表記法の見た目に関わる部分、そして数学の思考や数学オブジェクトの内容に関する部分の両方を符号化するというニーズをうまく満たすことです。
A fundamental challenge in defining a markup language for mathematics on
the Web is reconciling the need to encode both the presentation of a
mathematical notation and the content of the mathematical idea or object
which it represents.
数学の表記と数学的な思考との間の関係は、微妙で奥深いものです。形式的に言うと、記号による論理体系とそれらが形作る現象の対応関係について、数学的な理論のために混乱するような疑問が生じてしまいます。
もっと直感的な言い方をするならば、数学の表記法を利用する者なら誰しも、表記の選択の善し悪しによって生じる差についてよく知っています。
表記法の記号上の構造は、論理上の構造をも示唆しているのです。
たとえば、次のような微分のライプニッツ記法によって、分数の記号的な約分という計算の連鎖法則が「示唆」されます: 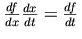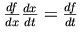
The relationship between a mathematical notation and a mathematical idea
is subtle and deep. On a formal level, the results of mathematical logic
raise unsettling questions about the correspondence between systems of
symbolic logic and the phenomena they model. At a more intuitive level,
anyone who uses mathematical notation knows the difference that a good
choice of notation can make; the symbolic structure of the notation
suggests the logical structure. For example, the Leibniz notation for
derivatives `suggests' the chain rule of calculus through the
symbolic cancellation of fractions: 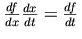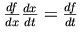 .
.
数学者や教師であれば、問題の重要な部分を際だたせる表記を選び、その他の情報を隠蔽したり小さく扱うことによって自分の専門知識が成り立っていることを直感的に知っているでしょう。
数学や科学の世界では、何かを技術的に厳密に表現する場合に、文章として書くことが常識として知られています。
つまり、ごちゃごちゃと詳細を正確に伝えようと言葉数を多くするよりは、表記を選んだほうが、よりよく相手に伝わるということです。
Mathematicians and teachers intuitively understand this very well; part
of their expertise lies in choosing notation that emphasizes key aspects of
a problem while hiding or diminishing extraneous aspects. It is
commonplace in mathematics and science to write one thing when strictly
technically something else is meant, because long experience shows this
actually communicates the idea better at some higher level than rigorous
detail.
しかし、普通は数学の記法は、数学オブジェクトの微妙な意味を完全に符号化するために用いられます。
数学の記法を用いればかなり正確に伝えることができますし、注意深く使用すれば、事実上曖昧さを完全に取り除くことができます。
さらに、曖昧さを含まないので、数学オブジェクトをコンピュータ代数システムや音声レンダラーなどのソフトウェア・アプリケーションで利用できるように記述することもできます。
このようにアプリケーション間の通信に主眼をおいたとき、見た目で伝わるニュアンスは、一般的にほとんど役割を果たしません。
In many other settings, though, mathematical notation is used to encode
the full, precise meaning of a mathematical object. Mathematical notation
is capable of prodigious rigor, and when used carefully, it can be
virtually free of ambiguity. Moreover, it is precisely this lack of
ambiguity which makes it possible to describe mathematical objects so that
they can be used by software applications such as computer algebra systems
and voice renderers. In situations where such inter-application
communication is of paramount importance, the nuances of visual
presentation generally play a minimal role.
MathML があれば、制作者は数学オブジェクトを記述する記法と、オブジェクトの数学的な構造自体との両方を符号化することができるようになります。
さらに、制作者は、見た目と数学的考えの中身の両方を明示化するために、これらを混合することも可能です。
この節の残りの部分では、それぞれ MathML がどのように使用されるかについて、基本的な考え方を示します。
MathML allows authors to encode both the notation which represents a
mathematical object and the mathematical structure of the object
itself. Moreover, authors can mix both kinds of encoding in order to
specify both the presentation and content of a mathematical idea. The
remainder of this section gives a basic overview of how MathML can be used
in each of these ways.
2.1.1 MathML 要素の分類
すべての MathML の要素は、プレゼンテーション要素、コンテンツ要素、そしてインターフェース要素、のいずれかのカテゴリーに帰属します。
それぞれのカテゴリーについては、第3章「プレゼンテーション マークアップ」、第4章「コンテンツ マークアップ」、MathML インターフェース で、それぞれ詳しく述べられています。
All MathML elements fall into one of three categories: presentation
elements, content elements and interface elements. Each of these categories
is described in detail in Chapter 3 [Presentation Markup], Chapter 4 [Content Markup]
and Chapter 7 [The MathML Interface], respectively.
プレゼンテーション要素は、数学の記法における視覚的な2次元的な構造を記述するものです。
この典型的な例としては、数式のパーツの水平的な並びを表す mrow 要素や、数式に対する上付文字を表す msup 要素が挙げられるでしょう。
一般的には、それぞれのプレゼンテーション要素は、行・列、上付・下付文字、のような表記上の「スキーマ」に対応しています。
すべての公式は、一つ一つを分解していくと、最終的には単純な構成要素 (数字や文字、あるいは記号など) に切り分けられます。
Presentation elements describe mathematical notation's visually oriented
two-dimensional structure. Typical examples are the
mrow
element, which is usually employed to indicate a
horizontal row of pieces of expressions, and the
msup element, which is used to mark up a base
expression and a superscript to it. As a general rule, each presentation
element corresponds to a single kind of notational `schema'
such as a row, a superscript, a subscript, an underscript and so on.
Any formula is made by putting together parts which ultimately can
be analyzed down to the simplest items such as digits, letters, or
other symbol characters.
今、数式表記における表示上の側面を考えましたが、プレゼンテーション・マークアップやコンテンツ・マークアップについても、同じように数学オブジェクトを分解することを考えることができます。
たとえばコンテンツ・マークアップを考えると、上付文字は、底と指数を引数とする累乗の演算を意味します。
これは偶然ではありません。
一般的には、数学表記のレイアウトは、数学オブジェクトにまつわる論理的な構造に従っているからです。
Although the previous paragraph was concerned with the display
aspect of mathematical notation, and hence with presentation markup,
the same observation about decomposition applies equally well to
abstract mathematical objects, and hence to content markup. For
example, in the context of content markup a superscript would
typically be denoted by an exponentiation operation that would require
two operands: a `base' and an
`exponent'. This is no coincidence, since as a general
rule, mathematical notation's layout closely follows the logical
structure of the underlying mathematical objects.
数学オブジェクトや数学の表記法における再帰的な性質は、MathML のマークアップに強く反映されています。
実際には、ほとんどのプレゼンテーション要素やコンテンツ要素は、元のオブジェクトを再帰的に構成するパーツに対応する別の MathML 要素を少なからず含むことがあります。
ベースとなるスキーマは一般に親スキーマと呼ばれ、構成部分は子スキーマと呼ばれます。
更に一般的には、MathML の表現はツリーとして認識することができます。
それぞれのノードは MathML の要素に対応し、「親」ノードにぶらさがる枝は「子」ノードに対応します。
それぞれのツリーの葉は、数字や文字といった最小の表記上ないし意味上の単位に対応します。
The recursive nature of mathematical objects and notation is strongly
reflected in MathML markup. In use, most presentation or content elements
contain some number of other MathML elements corresponding to the
constituent pieces out of which the original object is recursively
built. The original schema is commonly called the parent
schema, and the constituent pieces are called child
schemata. More generally, MathML expressions can be regarded as trees,
where each node corresponds to a MathML element, the branches under a
`parent' node correspond to its `children', and
the leaves in the tree correspond to atomic notation or content units such
as numbers, characters, etc.
MathML の表現ツリー中でのほとんどの葉ノードは、body のない 正規空要素 か、トークン要素 のどちらかになります。
正規空要素は、MathML の記号を直接的に表すもので、たとえばコンテンツ要素 <plus/> が該当します。MathML のトークン要素とは、MathML の要素のうちで唯一 MathML の文字データを含むことが許される要素のことです。
MathML の文字データは、Unicode 文字集合と、mglyph要素によって表現される特殊な文字集合から構成されます。
また、MathML の葉ノードとしては他に、MathML のフォーマットではない他のデータを保持するためのアノテーション要素が許されています。
Most leaf nodes in a MathML expression tree are either canonically
empty elements with no bodies, or token elements.
Canonically empty elements represent symbols directly in MathML, for
example, the content element
<plus/> does
this. MathML token elements are the only MathML elements permitted to
contain MathML character data. MathML character data consists of
Unicode characters with the infrequent addition of special
character constructions done with the
mglyph
element. A third kind of leaf node
permitted in MathML is the
annotation element,
which is used to hold data which is not in MathML format.
プレゼンテーション要素のトークン要素のうち、もっとも重要なものは識別子を表す mi 要素、数を表す mn 要素、そして演算子を表す mo 要素 の3つです。
常識的なレンダラーは、この種の文字データに対してはそれぞれ微妙に異なる植字スタイルを適用するでしょう:つまり、数字はuprightフェイス (訳注: normal とか roman な直立スタイルのこと)で、識別子は斜体で書かれるでしょうし、演算子は周囲に余分な空白を持つでしょう。
コンテンツ・マークアップにおいては、トークン要素には識別子を表す ci 要素、数字を表す cn 要素、その文書の中で新しく導入された記号を表す csymbol 要素の 3 つしかありません。
コンテンツ・マークアップ中ではその他の要素は一般に関数や演算子に用いられます。
apply 要素は、基本セットに対するユーザー定義の拡張を表すために提供されています。
The most important presentation token elements are
mi,
mn and
mo for representing identifiers, numbers and operators
respectively. Typically a renderer will employ slightly different
typesetting styles for each of these kinds of character data: numbers are
usually in upright font, identifiers in italics, and operators have extra
space around them. In content markup, there are only three tokens,
ci,
cn and
csymbol, for identifiers, numbers and new symbols
introduced in the document itself, respectively. In content markup,
separate elements are provided for commonly used functions and
operators. The
apply element is provided for
user-defined extensions to the base set.
マークアップの上では、ほとんどの MathML 要素は開始タグと終了タグによって記述され、その本体を表すマークアップを囲みます。
本体は、トークン要素の場合は文字データであり、他の場合は一般に子要素になります。
先ほど正規空要素と呼んだ 3 種類目の要素においては、本体は必要としないので、<name/> という形で記述されます。
この種の例としては、コンテンツ・マークアップの <plus/> 要素があります。
In terms of markup, most MathML elements are denoted by a
start tag and an end tag, which enclose the
markup for their contents. In the case of tokens, the content is
character data, and in most other cases, the content is the markup for
child elements. Elements in a third category, called canonically empty
elements, do not require any contents, and are denoted by a single tag of
the form <name/>. An example of this kind of
markup is <plus/> in content markup.
(a + b)2
という非常に簡単な例で、上で述べた考え方が実際にどのように利用されているか見てみましょう。
プレゼンテーション・マークアップでは例えば以下のようにマークアップされます:
Let us take the very simple example of (a +
b)2, and we can now see how the
principles discussed above play out in practice. One form of
presentation markup for this example is:
<mrow>
<msup>
<mfenced>
<mrow>
<mi>a</mi>
<mo>+</mo>
<mi>b</mi>
</mrow>
</mfenced>
<mn>2</mn>
</msup>
</mrow>
この例では、いくつかのプレゼンテーション要素の例が示されています。
まず、1 番目の要素は mrow 要素で、非常に頻繁に使われます。
この要素は、水平に並べられた素材の列を記述するために用いられます。
<mrow> タグと </mrow> タグの間に含まれる本体は、mrow 要素の引数と考えることができます。
つまり、ここではすべての式が mrow 要素の本体として含有されているということです。
既に述べたように、ほとんどの式は副式に分割されます。
これらの副式は、また同様に mrow 要素に含まれていることがあります。
例えば上記の例では、a + b もまた mrow 要素に含まれています。
This example demonstrates a number of presentation elements. The first
element, one that is used a great deal is
mrow.
This element is used to denote a row of horizontally aligned material. The
material contained between the <mrow> and </mrow> tags is considered to be an argument to the mrow element. Thus the whole expression here is
contained in an mrow element. As previously noted,
almost all mathematical expressions decompose into subexpressions. These
subexpressions can, in turn, also be contained in an mrow element. For example, a + b is also contained in an
mrow.
mfenced 要素は、数式の周りの括弧 (大括弧{brace}、角括弧<bracket>、丸括弧(parenthesis)) を提供します。デフォルトでは丸括弧が使用されます。
The
mfenced element is used to provide fences
(braces, brackets, and parentheses) around formula material. It defaults
to using parentheses.
変数 a と b を表示するための mi 要素、+ 演算子をマークアップするための mo 要素の使い方に注意してください。
Note the use of the
mi element for displaying
the variables a and b and the
mo element for
marking the + operator.
msup 要素は、上付文字を含む表現のための要素で、2つの引数として底部 (ここでは (a+b) ) と 指数部 (ここでは 2)を順にとります。
The
msup element is for expressions involving
superscripts and takes two arguments, in order, the base expression (here,
(a+b)) and the exponent expression (here, 2).
同じ例をコンテンツ・マークアップで記述すると、以下のようになります:
The content markup for the same example is:
<mrow>
<apply>
<power/>
<apply>
<plus/>
<ci>a</ci>
<ci>b</ci>
</apply>
<cn>2</cn>
</apply>
</mrow>
ここで、apply 要素はコンテンツ要素の一つで、数式に演算を適用するということを意味します。
上の例では、累乗を表現する power 要素と、加算を表す plus 要素は、どちらも apply 要素によって空要素の形で適用されています。
ここで、2つの演算子は二つの引数をとり、とくに power 演算子においてはその順番が非常に大切であることに気がつくでしょう。
しかし、子の順番を決定的にしているのは、一つ目の子(つまり演算子)が残りの子を引数としてとるという apply 要素の使用方法によるのです。
Here, the
apply content element means apply an
operation to an expression. In this example, the power element (for exponentiation), which requires no
body, and the similar
plus element (for addition)
are both applied. Observe that both operators take two
arguments, the order being particularly significant in the case of the
power operator. But the order of the children is crucial in the use
of the apply since the first child, the operator,
takes as argument list the remaining ones.
また、変数 a と b をマークアップする ci 要素、数 2 をマークアップする cn 要素の使われ方に注意してください。
Note the use of the
ci element to mark up the
variables a and b, and the
cn element to mark up
the number 2.
2.1.2 プレゼンテーション・マークアップ
MathML のプレゼンテーション・マークアップは30ほどの要素からなっていて、50以上もの属性を受け付けます。
多くの要素は レイアウト・スキーマ に対応しており、他のプレゼンテーション要素を包括します。
それぞれのレイアウト・スキーマは、上付文字・下付き文字・分数や行列といった2次元の表示方法に対応しています。
その他にも、上で紹介した mi 要素、mo 要素、mn 要素をはじめとするトークン要素があります。
そして、位置揃えに関連した空要素も若干含まれています。
MathML presentation markup consists of about 30 elements which accept
over 50 attributes. Most of the elements correspond to layout
schemata, which contain other presentation elements. Each layout
schema corresponds to a two-dimensional notational device, such as a
superscript or subscript, fraction or table. In addition, there are the
presentation token elements
mi,
mo and
mn introduced above, as
well as several other less commonly used token elements. The remaining few
presentation elements are empty elements, and are used mostly in connection
with alignment.
レイアウト・スキーマは、いくつかの要素集団に分類されます。1つ目の要素集団はスクリプト(上付や下付)に関するもので、msub 要素や munder 要素、そして mmultiscripts 要素が含まれます。
もう1つは、より一般的なレイアウトに焦点を合わせた要素集合で、mrow 要素、mstyle 要素、mfrac 要素が含まれます。
また、行列を表現する要素集合があります。
さらに、maction 要素はそれ自身で要素集合を作り、たとえば数式中で二つの表記を切り替えるアクションのような、様々なアクションを表現することができます。
The layout schemata fall into several classes. One group of
elements is concerned with scripts, and contains elements such as
msub,
munder,
and mmultiscripts. Another group focuses on
more general layout and includes mrow, mstyle, and mfrac. A third group deals with tables.
The maction element is in a category by
itself, and allows coding of various kinds of actions on notation,
such as occur in an expression which toggles between two pieces of
notation.
多くのレイアウト・スキーマが持つ重要な特徴は、子スキーマの順番が意味を持つということです。
例えば、mfrac 要素の1つ目の子は分子を表し、2つ目の子は分母を表します。
子スキーマの順番は MathML DTD が XML レベルで規定しているものではありませんから、順番が持つ情報は MathML プロセッサーのみが利用でき、一般的な XML プロセッサーは適切に処理できません。
私たちが mfrac のような MathML 要素の特定の順番で子を求めることを強調する際には、その子のことを引数と呼び、mfrac 要素のことを表記上の「コンストラクター」と考えます。
An important feature of many layout schemata is that the order of child
schemata is significant. For example, the first child of an
mfrac element is the numerator and the second child is
the denominator. Since the order of child schemata is not enforced at the
XML level by the MathML DTD, the information added by ordering is only
available to a MathML processor, as opposed to a generic XML processor.
When we want to emphasize that a MathML element such as
mfrac requires children in a specific order, we will
refer to them as arguments, and think of the
mfrac element as a notational
`constructor'.
2.1.3 コンテンツ・マークアップ
コンテンツ・マークアップは、120ほどの要素から構成され、およそ1ダースの属性を受け付けます。
大部分の要素は空要素であり、様々な演算子や関係、特別な名が付いた関数などに対応しています。
この種の具体的な例としては、partialdiff 要素 や leq 要素、そして tan 要素があります。
他にも matrix 要素や set 要素は様々な数学上のデータ種を符号化するのに用いられます。
さらに、apply 要素のようなコンテンツ要素は重要なカテゴリーであり、演算を数式に適用し新しい数学オブジェクトを構成するのに用いられます。
Content markup consists of about 120 elements accepting roughly a dozen
attributes. The majority of these elements are empty elements corresponding
to a wide variety of operators, relations and named functions. Examples of
this sort include
partialdiff,
leq and
tan. Others such as
matrix and
set are used to
encode various mathematical data types, and a third, important category of
content elements such as
apply are used to apply
operations to expressions and also to make new mathematical objects from
others.
apply 要素はおそらく最も重要なコンテンツ要素でしょう。
apply 要素は、引数に対して関数や演算を適用するのに用いられます。
ここでも子スキーマの位置は重要で、1つ目の子が適用されるべき関数を表し、残りの子スキーマが関数への引数を表します。
プログラミング言語である LISP のように、apply 要素では常に前置式的な表現が用いられることに注意してください。特に、減算のような2値演算においても、2つの引数の前に減算演算子がマークアップされます。たとえば、a - b は次のようにマークアップされます:
The
apply element is perhaps the single most
important content element. It is used to apply a function or operation to a
collection of arguments. The positions of the child schemata are again
significant, with the first child denoting the function to be applied, and
the remaining children denoting the arguments of the function in
order. Note that the apply construct always uses
prefix notation, like the programming language LISP. In particular, even
binary operations such as subtraction are marked up by applying a prefix
subtraction operator to two arguments. For example, a -
b would be marked up as
<mrow>
<apply>
<minus/>
<ci>a</ci>
<ci>b</ci>
</apply>
</mrow>
関数や演算子によっては、1つ以上の数量詞が定義されてなければならないものがあります。
たとえば、定積分においては、被積分関数に加えて、積分の上下界と積分変数を明示しなければなりません。
こうした理由から、bvar や lowlimit といった限定スキーマが用意されています。
これらの要素は diff や int といった演算子とともに用いられます。
A number of functions and operations require one or more quantifiers to
be well-defined. For example, in addition to an integrand, a definite
integral must specify the limits of integration and the bound variable. For
this reason, there are several qualifier schemata such as
bvar and
lowlimit. They are
used with operators such as
diff and
int.
数式処理システムが解析するコンテンツ・マークアップの中では、declare 構文が特に大切です。
declare 要素は、基本的な割り当てメカニズムを提供し、変数の型や値を宣言することができます。
The
declare construct is especially important
for content markup that might be evaluated by a computer algebra system.
The declare element provides a basic assignment
mechanism, where a variable can be declared to be of a certain type, with a
certain value.
プレゼンテーション・マークアップとコンテンツ・マークアップの両方の例では、数学的な表現は再帰的に入れ子構造をとっていました。より単純な MathML の要素によってそれぞれの階層が分解されました。次のセクションの例では、より複雑な表現でこれを説明します。
In both the presentation and content markup examples, mathematical
expressions are recursively decomposed into nested, simpler MathML
elements specifying each stage of the decomposition. The examples in
the following sections illustrate this with more complex expressions.
2.1.4 プレゼンテーションとコンテンツの混在
種類の異なるマークアップには、それぞれもっとも適切なタスクがあります。
ワールド・ワイド・ウェブが市民権を得る前に書かれた文書は、たいていの場合は視覚の上での情報通信のみを目的としていました。
従って、従来のデータはおそらく単純なプレゼンテーション・マークアップに変換するのが最適でしょう。
また、それ故、筆者が意味しようとした意味情報は、発見的手法で推測することしかできません。
対照的に、数学アプリケーションや教育系のオーサリングツールは、完全にコンテンツ・マークアップを主体とした記述を好むでしょう。
大半のアプリケーションは、これら両極のいずれかの間に分類できます。
こうした中間的なアプリケーションでは、最適なマークアップはプレゼンテーション・マークアップとコンテンツ・マークアップを混在したものとなります。
Different kinds of markup will be found most appropriate for different
kinds of tasks. Documents written before the World Wide Web became
important were most often intended only for visual communication of
information, so that legacy data is probably best translated into pure
presentation markup, since semantic information about what the author meant
can only be guessed at heuristically. By contrast, some mathematical
applications and pedagogically-oriented authoring tools will likely choose
to be entirely content-based. The majority of applications fall somewhere
in between these extremes. For these applications, the most appropriate
markup is a mixture of both presentation and content markup.
プレゼンテーション・マークアップとコンテンツ・マークアップを混在させる上での規則は、混在したコンテンツは意味のある箇所でのみ利用が許されるべき、という一般的な原則から派生しています。
つまり、プレゼンテーション・マークアップの中に埋められたコンテンツ・マークアップについて言えば、それぞれのコンテンツ・マークアップの断片は数学的に意味があるものでなければならないし、完全に記述するためにそれ以上引数や数量詞を必要としてはならないということです。
逆にコンテンツ・マークアップの中のプレゼンテーション・マークアップで言えば、プレゼンテーションマークアップは、トークン要素に含まれているべきであるということで、このことにより、それぞれの表記上の単位が変数や関数の名前として使われていると解釈されます。
The rules for mixing presentation and content markup derive from the
general principle that mixed content should only be allowed in places where
it makes sense. For content markup embedded in presentation markup this
basically means that any content fragments should be semantically
meaningful, and should not require additional arguments or quantifiers to
be fully specified. For presentation markup embedded in content markup,
this usually means that presentation markup must be contained in a content
token element, so that it will be treated as an indivisible notational unit
used as a variable or function name.
また、semantics 要素を使うという方法もあります。
semantics 要素は、MathML の表現に様々な種類の注釈を結びつけるための要素です。
semantics 要素の一般的な使われかたは、コンテンツ・マークアップを他のプレゼンテーション・マークアップに意味上の注釈として結びつけることです。
この方法を利用すれば、あるコンテンツ・マークアップを表現する際に標準ではない表記で明示することができます。
その他にも semantics 要素を利用すれば、OpenMath の表記など、他の意味的な明細を MathML の表記に組み込むことができます。
こうして、semantics 要素は MathML のコンテンツ・マークアップの視野を拡げることができます。
Another option is to use a
semantics element.
The semantics element is used to bind MathML
expressions to various kinds of annotations. One common use for the semantics element is to bind a piece of content markup
to some presentation markup as a semantic annotation. In this way, an
author can specify a non-standard notation to be used when displaying a
particular content expression. Another use of the semantics element is to bind some other kind of
semantic specification, such as an OpenMath expression, to a MathML
expression. In this way, the semantics element can
be used to extend the scope of MathML content markup.
2.2 文書中の MathML
上の議論は、他の文書中という状況を考えずに、数式の断片について考えてきました。
より詳細な話をするために、プログラム言語で言う「Hello World!」に該当する現実的な例を見ていくことにしましょう。
ここでは、先ほど出てきた、"2変数の和の2乗" を含む XHTML 1.0 文書 について、より完全なコードを示してみましょう。コードは、以下のようになります。
The discussion above has actually been of fragmentary formulas
outside the context of any document. To be more specific let us look
at what corresponds to a programming language's "Hello
World!" example. We shall provide more complete code for an XHTML 1.0
document containing the square of a sum of two variables
mentioned above. It would be
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<title>MathML's Hello Square</title>
</head>
<body>
<p> This is a perfect square:</p>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<msup>
<mfenced>
<mrow>
<mi>a</mi>
<mo>+</mo>
<mi>b</mi>
</mrow>
</mfenced>
<mn>2</mn>
</msup>
</mrow>
</math>
</body>
</html>
ここでは、一般的な XHTML 文書の構造を示しました。
最初の開始タグ <html> は、XML の名前空間宣言と言語情報によって修飾されています。
次に、習慣としてタイトルを含む head 要素が続きます。
そして、<body> タグにも名前空間宣言があり、ここで 標準的な MathML の名前空間を示す m という省略された前置詞を宣言しています。
次に単純な段落があり、そしてようやく名前空間の関連づけ宣言を含む math 要素が出てきます。
math 要素の中には、私たちが使おうとしている MathML マークアップが含まれています。
MathML を使うのにこれほど複雑な名前空間を使わなければならない理由については、第7章「MathML のインターフェイス」で説明されています。
これは現在の XML を扱う技術の限界に関係するものであり、いずれ制限はなくなると思われます。
Here we have the normal structure of an XHTML document. It begins
with the start tag <html> embellished with an
XML namespace declaration and language assertions. A head element contains a title as is customary.
Then the <body> beginning also has a namespace
declaration of an abbreviative prefix letter m
to be used for the standard MathML namespace. Next comes a simple
paragraph. Finally we get the math element
which also has a namespace association declared. Inside the math element is MathML markup as we are beginning
to be used to it. The reasons why one might have to do a more complex
namespace declaration for MathML are explained in Chapter 7 [The MathML Interface]; they have to do with present-day limitations in some XML
handling, that may be expected to go away.
また、!DOCTYPE 宣言のような高度な技術的な詳細についても、やはり第7章「MathMLのインターフェイス」にある議論をご参照下さい。
For the next level of technical detail concerning such matters
as !DOCTYPE statements and the like, see the
discussion in Chapter 7 [The MathML Interface].
2.3 MathML の例
今後は、実際の文書内の math 要素中に現れる MathML の断片という形で例を挙げてみましょう。
本質を明確に説明するために、第3章以降でも、すべてこのように MathML の断片という形で例を挙げています。
We continue below to display examples in the form of fragments of
MathML markup such as would appear inside math
elements in real documents. For the sake of clearer exposition of
principles, the examples in Chapters 3, 4, 5 and 6 follow this form of
giving examples as MathML fragments.
2.3.1 プレゼンテーション・マークアップの例
表記: x2 + 4x + 4 = 0.
マークアップ:
<mrow>
<mrow>
<msup>
<mi>x</mi>
<mn>2</mn>
</msup>
<mo>+</mo>
<mrow>
<mn>4</mn>
<mo>⁢</mo>
<mi>x</mi>
</mrow>
<mo>+</mo>
<mn>4</mn>
</mrow>
<mo>=</mo>
<mn>0</mn>
</mrow>
入れ子になった mrow 要素の使用方法に注意してください。
例えば 1 つ目の mrow は、数式の左辺が「=」の演算対象として機能している、ということを示しています。
それぞれの項のマークアップは、視覚的なレンダリングの上で空白の処理を可能にしたり、音声表現での"溜め"を表現したり、改行の処理を容易にしたりできます。
InvisibleTimes は MathML 文字実体の一つで、ここではレンダラーに対し、4 と x の間に特別な空白規則があり、さらに 4 と x は別々の行に切り分けられるべきではないと言うことを示唆しています。
ただし、この実体の利用方法は MathML 1.0 で導入されたものでしたが、実際は今後あまり推奨されるものではありません。
究極的には、すべての標準的な文字データは Unicode 値で与えられるべきなのです。
しかし、⁢ を表す文字が Unicode 3.2 で導入が期待され、さらにその文字コードが Unicode Amendment で考察されてはいるものの、現状で利用されている Unicode 3.0 の文字には ⁢ に該当する文字が存在していません。
ここで予定されている数字による文字参照 ࠎ を利用することもできますが、以降の例でも明確にするために実体参照を利用することにします。
このことに関しては、第3.2節「トークン要素」 と 第6章「文字、実体とフォント」 ではっきりと議論されています。
Note the use of nested mrow elements to denote terms, for
example, the left-hand side of the equation functioning as an operand
of `='. Marking terms greatly facilitates spacing for
visual rendering, voice rendering, and line breaking. The InvisibleTimes MathML character entity is used here
to indicate to a renderer that there are special spacing rules between
the 4 and the x, and that the 4 and the x should not be broken onto
separate lines. In fact, this use of an entity which was introduced
in MathML 1.0 is no longer the way that is preferred. Ultimately all
ordinary character data is given by Unicode values. However, although
a character for ⁢ is expected in
Unicode 3.2, and there is a suggested code point under
consideration in a Unicode amendment, there is no Unicode 3.0
character to be used at present. We could use the expected numerical
character reference ࠎ but for clarity we will continue to
use entity references in these examples. The situation is explicitly
discussed in Section 3.2 [Token Elements] and in Chapter 6 [Characters, Entities and Fonts].
表記:
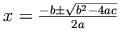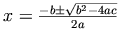 .
.
マークアップ:
<mrow>
<mi>x</mi>
<mo>=</mo>
<mfrac>
<mrow>
<mrow>
<mo>-</mo>
<mi>b</mi>
</mrow>
<mo>±</mo>
<msqrt>
<mrow>
<msup>
<mi>b</mi>
<mn>2</mn>
</msup>
<mo>-</mo>
<mrow>
<mn>4</mn>
<mo>⁢</mo>
<mi>a</mi>
<mo>⁢</mo>
<mi>c</mi>
</mrow>
</mrow>
</msqrt>
</mrow>
<mrow>
<mn>2</mn>
<mo>⁢</mo>
<mi>a</mi>
</mrow>
</mfrac>
</mrow>
mfrac 要素と msqrt 要素は、それぞれ分数と二乗根を生成するために利用されています。
The
mfrac and
msqrt
elements are used for generating fractions
and square roots, respectively.
「プラスマイナス」記号は、既に Unicode 文字 �B1; ですでに導入されているにも拘わらず、特別な実体名 ± で与えられていることに注意してください (訳注: つまり、JIS X 208 でも「±」という表現が可能だけれども ± という表記を使え、ということです) 。
MathML では、数学記号に対しわかりやすい文字名のリストが用意されています。
画面上の描画や印刷に必要な数学記号に加え、音声レンダリングでも利用できるように記号を用意しています。
なぜこれが重要かというと、音声レンダリングでは、
Notice that the `plus or minus' sign is given by a special
entity name ±, though in this case there
already is a Unicode character �B1;.
MathML provides a very comprehensive list of character names for
mathematical symbols. In addition to the mathematical symbols needed for
screen and print rendering, MathML provides symbols to facilitate audio
rendering. For audio rendering, it is important to be able to
automatically determine whether
<mrow>
<mi>z</mi>
<mfenced>
<mrow>
<mi>x</mi>
<mo>+</mo>
<mi>y</mi>
</mrow>
</mfenced>
</mrow>
という表記が「z と x の積に y を足す」とも「z に x と y の和をかける」とも読み上げられうるからです。
また、⁢ (U+2062) と ⁡ (U+2061) を利用すれば、音声レンダラーのために区別方法を直接符号化して含めることができます。
例えば、⁢ (U+2062) は、z を含む行の後に付け足すことができます。
MathML では、たとえば ⅆ (U+2146) という実体で「微分記号の d 」を表現することができるようになっており、微妙な空白処理がされて描画されたり、「d」だとか「差分の d」などと読み上げられたりできるようになっています。
つまり、曖昧さを減らすためにコンテンツ・マークアップを始めとする他のメカニズムを用いないのであれば、これらの文字を実体参照の形で表して、文書をよりアクセシブルにするべきです。
should be read as `z times the quantity x plus
y' or `z of x plus y'. The
characters ⁢ (U+2062) and ⁡ (U+2061) provide a way for authors to
directly encode the distinction for audio renderers. For instance, in
the first case ⁢ (U+2062) should
be inserted after the line containing the z. MathML also
introduces entities like ⅆ (U+2146)
representing a `differential d', which renders with slightly
different spacing in print and can be rendered as `d' or
`with respect to' in speech. Unless content tags, or some
other mechanism, are used to eliminate the ambiguity, authors should
always use these characters here referred to as entities, in order to
make their documents more accessible.
表記:
![A=\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]](image/f2008.gif) .
.
マークアップ:
<mrow>
<mi>A</mi>
<mo>=</mo>
<mfenced open="[" close="]">
<mtable>
<mtr>
<mtd><mi>x</mi></mtd>
<mtd><mi>y</mi></mtd>
</mtr>
<mtr>
<mtd><mi>z</mi></mtd>
<mtd><mi>w</mi></mtd>
</mtr>
</mtable>
</mfenced>
</mrow>
mtable 要素は、MathML の表が生成されることを意味します。
mtr 要素は表中の行を示し、mtd 要素は行の要素としてのデータを保持します。
ほとんどの要素は、画面上ないし印刷上の描画に対する詳細な制御を行う属性を持っています。
たとえば、mfenced 要素の属性の中には 上記のグループ化された表現の開始と終端でどのような区切り文字を使うのかを制御する属性があります。
<mo> によって与えられる演算子要素の属性の標準値は、辞書によって与えられています。
MathML で期待される演算子の辞書に関しては、付録 F「演算子辞書」 を参してください。
The mtable element denotes that a
MathML table is being created. The mtr
specifies a row of the table and the mtd
element holds the data for an element of a row. Most elements have a
number of attributes that control the details of their screen and
print rendering. For example, there are several attributes for the mfenced element that controls what delimiters
should be used at the beginning and the end of the grouped expression
above. The attributes for operator elements given using <mo> are set to default values determined by a
dictionary. For the suggested MathML operator dictionary, see Appendix F [Operator Dictionary].
2.3.2 コンテンツ・マークアップの例
表記: x2 + 4x + 4 = 0.
マークアップ:
<mrow>
<apply>
<eq/>
<apply>
<plus/>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
</apply>
<apply>
<times/>
<cn>4</cn>
<ci>x</ci>
</apply>
<cn>4</cn>
</apply>
<cn>0</cn>
</apply>
</mrow>
apply 要素が関係、演算子、関数を表していることに気を付けましょう。
Note that the apply element is used for
relations, operators and functions.
表記:
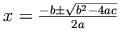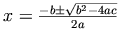 .
.
マークアップ:
<mrow>
<apply>
<eq/>
<ci>x</ci>
<apply>
<divide/>
<apply>
<mo>±</mo>
<apply>
<minus/>
<ci>b</ci>
</apply>
<apply>
<root/>
<apply>
<minus/>
<apply>
<power/>
<ci>b</ci>
<cn>2</cn>
</apply>
<apply>
<times/>
<cn>4</cn>
<ci>a</ci>
<ci>c</ci>
</apply>
</apply>
<cn>2</cn>
</apply>
</apply>
<apply>
<times/>
<cn>2</cn>
<ci>a</ci>
</apply>
</apply>
</apply>
</mrow>
MathML のコンテンツ・マークアップには、「プラスマイナス」の演算を表す要素は直接的には含まれていません (訳注: なぜなら、プラスマイナスを表現する実質的な演算は存在しないからであり、プラスマイナスはあくまで表現上の省略に過ぎないからです)。
そこで mo 要素を使い、プレゼンテーション・マークアップであるこの演算子をコンテンツ・マークアップの演算子として機能させようとしているのです。
これは、プレゼンテーション・マークアップとコンテンツ・マークアップを混在させてコンテンツ・マークアップを拡張する方法の例でもあるのです。
MathML content markup does not directly contain an element for the
`plus or minus' operation. Therefore, we use the mo element to declare that we want the presentation
markup for this operator to act as a content operator. This is a simple
example of how presentation and content markup can be mixed to extend
content markup.
表記:
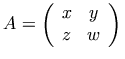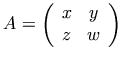 .
.
マークアップ:
<mrow>
<apply>
<eq/>
<ci>A</ci>
<matrix>
<matrixrow>
<ci>x</ci>
<ci>y</ci>
</matrixrow>
<matrixrow>
<ci>z</ci>
<ci>w</ci>
</matrixrow>
</matrix>
</apply>
</mrow>
ここでは matrix 要素と matrixrow 要素を使い、行列における行の項目を包んでいます。
標準では、コンテンツ要素である matrix 要素は周囲の括弧を含んでいるので、括弧を明示的に符号化する必要がないことに注意しましょう。
この点は、プレゼンテーション要素である mtable 要素が行列も単なる表も符号化できるが故に、必要に応じて明示的に括弧を符号化しなければならなかった点とは大きく異なっています。
Here we have used the matrix element, and the
matrixrow element to wrap the entries in a row of
the matrix. Note that, by default, the rendering of the content
element matrix includes enclosing parentheses,
so we need not directly encode them. This is quite different from the
presentation element mtable which may or may
not refer to a matrix, and hence requires explicit encoding of
parentheses if they are desired.
2.3.3 混在したマークアップの例
表記:
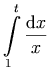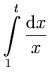 .
.
マークアップ:
<mrow>
<semantics>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>t</mi>
</msubsup>
<mfrac>
<mrow>
<mo>ⅆ</mo>
<mi>x</mi>
</mrow>
<mi>x</mi>
</mfrac>
</mrow>
<annotation-xml encoding="MathML-Content">
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>1</cn></lowlimit>
<uplimit><ci>t</ci></uplimit>
<apply>
<divide/>
<cn>1</cn>
<ci>x</ci>
</apply>
</apply>
</annotation-xml>
</semantics>
</mrow>
この例では、コンテンツ・マークアップによる表現を「意味上の注釈」としてプレゼンテーション・マークアップに追加するために、semantics 要素を使っています。
表示上のマークアップでは、たとえば積分記号に相当する数式に対し、subsup 要素を利用して下付き文字と上付文字を付加しています。
また、∫ や ⅆ という実体を使って積分記号や微分記号を表しています。
In this example, we use the semantics
element to provide a MathML content expression to serve as a
`semantic annotation' for a presentation expression. In
the display markup, we have used the msubsup
element to attach a subscript and a superscript to an expression, in
this case the integral sign. We also used entities ∫ and ⅆ to specify the
integral and differential symbols.
semancics 要素は、その1つ目の子による表現を注釈される対象として扱い、それ以降の子を注釈として扱います。注釈の種類に関しては全く制限がありません。たとえば、自動数式システムで利用するために TEX の符号化を利用することもできます。
注釈の種類については encoding 属性と annotation 要素および annotation-xml 要素によって特定されます。
The semantics element has as its first child
the expression being annotated, and the subsequent children are the
annotations. There is no restriction on the kind of annotation that
can be attached using the semantics element.
For example, one might give a TEX encoding, or computer algebra
input in an annotation. The type of annotation is specified by the encoding attribute and the annotation and annotation-xml elements.
他にも semantics 要素は、コンテンツ・マークアップによる表現を使う際にその表記を示唆する状況で、よく利用されるでしょう。
そのような状況では、上で挙げられた数式は以下のようなマークアップになるでしょう:
Another common use of the semantics
element arises when one wants to use a content coding, and
provide a suggestion for its presentation. In such a case,
applied to the formula above we would have the markup:
<semantics>
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>1</cn></lowlimit>
<uplimit><ci>t</ci></uplimit>
<apply>
<divide/>
<cn>1</cn>
<ci>x</ci>
</apply>
</apply>
<annotation-xml encoding="MathML-Presentation">
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>t</mi>
</msubsup>
<mfrac>
<mrow>
<mo>ⅆ</mo>
<mi>x</mi>
</mrow>
<mi>x</mi>
</mfrac>
</mrow>
</annotation-xml>
</semantics>
コンテンツ・マークアップの標準的な符号化による描画が望まれないとき、こうした注釈の方法は非常に便利です。
たとえば、標準ではレンダラーによっては上記の被積分関数を「(1/x) dx」と表現するでしょう。被積分関数を「dx/x」と表現することを望んでいることを明示するために、上記のような MathML のプレゼンテーション・マークアップによる注釈を利用するのです。
ただし、レンダラーは必ずしも注釈に含まれる情報に配慮する必要はなく、その情報が利用されるかどうかはレンダラーに依存している、ということに注意してください。
This kind of annotation is useful when something other than the default
rendering of the content encoding is desired. For example, by default, some
renderers might layout the integrand something like `(1/x)
dx'. Specifying that the integrand should by preference
render as `dx/x' instead can be accomplished
with the use of a MathML Presentation annotation as shown. Be aware,
however, that renderers are not required to take into account information
contained in annotations, and what use is made of them, if any, will depend
on the renderer.
2.4 MathML の構文と文法
2.4.1 MathML の構文と文法
MathML は [XML] (Extensible Markup Language; 拡張可能なマークアップ言語) の応用の一つであり、それ故その構文は XML 構文規則に支配され、その文法の一部は DTD (Document Type Definition; 文書型定義) によって特定化されておます。
言い換えれば、タグや属性、実体参照などの使用に関する詳細は XML 言語使用によって定められており、要素がそれぞれ入れ子構造になるなどといった MathML の要素と属性名に関する詳細は MathML DTD で特定化されていると言うことです。
MathML DTD は 付録 A「MathML のパース」 にあります。
MathML is an application of [XML], or Extensible
Markup Language, and as such its syntax is governed by the rules of
XML syntax, and its grammar is in part specified by a DTD, or Document
Type Definition. In other words, the details of using tags,
attributes, entity references and so on are defined in the XML
language specification, and the details about MathML element and
attribute names, which elements can be nested inside each other, and
so on are specified in the MathML DTD. This is in Appendix A [Parsing MathML].
W3C は XML をウェブで利用するために柔軟性を加える方法を考え、XML を基本とする応用がモジュール化されることを推奨していましたが、DTD の基本的な形式が十分に柔軟ではないと認識しました。
そこで、DTD に取って代わる仕様文書である XML スキーマ [XMLSchemas] の仕様策定のために W3C ワーキングループが結成されました。
MathML 2.0 は、進化しているウェブ技術の最新の随を数学が生かせるような設計を意識しています。
MathML のスキーマに関してのより詳しい情報については、付録 A「MathMLのパース」 および MathML のホームページ を参照してください。
The W3C in seeking to increase the flexibility of the use of XML
for the Web, and to encourage modularization of applications built
with XML, has found that the basic form of a DTD is not sufficiently
flexible. Therefore, a W3C Working Group was created to develop a
specification for XML Schemas [XMLSchemas], which are
specification documents that will eventually supersede DTDs. MathML
2.0 is consciously designed so that mathematics may take advantage of the
latest in the evolving Web technology. Thus, there is to be a schema
for MathML. For further information on a MathML schema see Appendix A [Parsing MathML] and the MathML
Home Page.
しかし、XML 応用として継承した一般的な規則に加え、MathML は構文規則と文法規則を新しく定めています。
MathML では、これらの規則を利用することで、多くの要素を導入し複雑な DTD やスキーマを書くことなく、純粋な XML 以上に多くの情報を符号化できるようになっています。
コンテンツ・マークアップの表現上の文法に関しては、付録 B「コンテンツ・マークアップ: 有効な文法」 を参照してください。
当然ながら、MathML で導入された規則を利用する上での欠点は、一般的な XML プロセッサーや評価エンジン (Validator) にはそれが判らないということです。
However, MathML also specifies some syntax and grammar rules in addition
to the general rules it inherits as an XML application. These rules allow
MathML to encode a great deal more information than would ordinarily be
possible with pure XML, without introducing many more elements, and using a
substantially more complex DTD or schema. A grammar for content markup
expressions is given in Appendix B [Content Markup Validation Grammar]. Of course, one drawback to
using MathML specific rules is that they are invisible to generic XML
processors and validators.
MathML で追加された構文と文法規則は、主に2つに分類されます。
1つは属性値に付加的な基準を課すものです。
たとえば純粋な XML では属性値が必ず正整数であることを要求できません。
もう1つは、 DTD やスキーマでは指定できない、並び順のような子要素への詳細な制限を指定するものです。
たとえば、純粋な XML では一つ目の子と2つ目の子とで解釈を変えることができません。
There are basically two kinds of additional MathML grammar and syntax
rules. One kind involves placing additional criteria on attribute values.
For example, it is not possible in pure XML to require that an attribute
value be a positive integer. The second kind of rule specifies more
detailed restrictions on the child elements (for example on ordering) than
are given in the DTD or even a schema. For example, it is not possible in
XML to specify that the first child be interpreted one way, and the second
in another.
以下のセクションでは、一般的な XML の構文と文法の特徴とともに、特に MathML のそれについて議論します。
MathML 仕様書の残りの部分を通じて、使用方法が XML の構文と MathML DTD (とスキーマ) のどちらによって要請されるのか、あるいは MathML の独自な規則によるのか、についての区別には気を付けています。
ただし、どの規則に違反しているのかを区別せずに「MathML の誤り」と言及することもあり得ますので、ご了承下さい。
The following sections discuss features both of XML syntax and grammar
in general, and of MathML in particular. Throughout the remainder of the
MathML specification, we will usually take care to distinguish between
usage required by XML syntax and the MathML DTD (and schema) and usage
required by MathML specific rules. However, we will frequently allude to
`MathML errors' without identifying which part of the
specification is being violated.
2.4.2 XML 構文入門
MathML は XML の応用である以上、MathML の仕様書は XML の専門用語を使用して記述されます。
たとえば、XML のデータは従来の ASCII 文字を含む Unicode 文字によって構成されますし、< などのような「実体参照」(非公式には「実体」と略するときもある) は主に「拡張文字」を表すために用いられます。
「要素」は <mi fontstyle="normal"> x </mi> のような部分のことを指します。
Since MathML is an application of XML, the MathML specification uses the
terminology of XML to describe it. Briefly, XML data is composed of Unicode
characters (which include ordinary ASCII characters), `entity
references' (informally called `entities') such as < which usually represent `extended
characters', and `elements' such as <mi
fontstyle="normal"> x </mi>.
要素は HTML のように、通常は他の「本体」と呼ばれる XML データを、「開始タグ」と「終了タグ」によって囲んでいます。
他にも <plus/> のように、本体や終了タグが含まれないと言うことを示すために、開始タグが /> で終わった要素のことを「空要素」と呼びます。
また、開始タグには「属性」と呼ばれる名前付きのパラメーターがあり、上記の例では fontstyle="normal" がそれにあたります。XML の詳細については、XMLの仕様を参照してください [XML] 。
An element quite often encloses other XML data called its
`content', or `body', between a `start
tag' (sometimes called a `begin tag') and an `end
tag', much as in HTML. There are also `empty elements'
such as <plus/>, whose start tag ends with
/> to indicate that the element has no content or end
tag. The start tag can contain named parameters called
`attributes', such as fontstyle="normal" in the
example above. For further details on XML, consult the XML specification
[XML].
XML では大文字と小文字を区別しますので、やはり MathML においても要素と属性名は大文字と小文字が区別されます。
読みやすさの都合上、MathML 仕様書ではそれらの多くを小文字で定義しています。
As XML is case-sensitive, MathML element and attribute names are
case-sensitive. For reasons of legibility, the MathML specification
defines them almost all in lowercase.
XML マークアップの公式な議論の中では、要素とタグは厳密に区別されています。
ここで、要素とは mrow のようなものを、タグとは <mrow> や </mrow> のようなものを指します。
要素の中において、<mrow> 開始タグと </mrow> 終了タグの間にあるものは本体と呼ばれます。
「空要素」とは、たとえば none 要素のように本体を含まないものと定義され、<none/> という形式のタグを一つだけとります。
この仕様書の中では通常、要素とタグの区別はあまり明確に書かれていません。
たとえば、<mrow> と </mrow> は実際には要素のうちのタグでしかありませんが、要素と属性のどちらに言及しているかを見た目で区別するために、単に要素と記述することもあります。
もちろん、「要素」「タグ」という言葉自身は、XML の用語に従って厳密に区別されています。
In formal discussions of XML markup, a distinction is maintained
between an element, such as an mrow element,
and the tags <mrow> and </mrow> marking it. What is between the <mrow> start tag and the </mrow> end tag is the content, or body, of the mrow element. An `empty element'
such as none is defined to have no body, and
so has a single tag of the form <none/>.
Usually, the distinction between elements and tags will not be so
finely drawn in this specification. For instance, we will sometimes
refer to the <mrow> and <none/> elements, really meaning the elements whose
tags these are, in order that references to elements are visually
distinguishable from references to attributes. However, the words
`element' and `tag' themselves will be used
strictly in accordance with XML terminology.
2.4.3 子と引数
MathML 要素の多くは、必要とする子要素の数が限られていたり、特定の位置の子要素に特別な意味を付加したりします。
既に述べたように、これらの要請は MathML 独自のものであり、XML の構文や文法だけでは完全には与えられません。
MathML 要素の子がこうした付加的な条件に応じるとき、これを単に「子」と呼ばずに 引数 と呼ぶことで MathML の独自の使い方であることを強調しています。
特に 第3章「プレゼンテーション・マークアップ」 では、「引数」という言葉が特別な言及なしにこういった技術的な意味で用いられ、子要素と区別されていることに注意してください。
Many MathML elements require a specific number of child elements or
attach additional meanings to children in certain positions. As noted
above, these kinds of requirements are MathML specific, and cannot be
given entirely using XML syntax and grammar. When the children of a
given MathML element are subject to these kinds of additional
conditions, we will often refer to them as arguments
instead of merely as children, in order to emphasize their MathML
specific usage. Note that, especially in Chapter 3 [Presentation Markup], the
term `argument' is usually used in this technical sense,
unless otherwise noted, and therefore refers to a child element.
MathML 仕様書を通じて、各要素ごとの構文の詳しい議論においては、大抵はその名前から必要とする引数の数とその順序を暗に読みとることができます。
この情報は、プレゼンテーション要素については 第3.1.3節「必要な引数」 で、コンテンツ要素については 付録 B「コンテンツ・マークアップの有効な文法」 に掲出されています。
In the detailed discussions of element syntax given with each
element throughout the MathML specification, the number of required
arguments and their order is implicitly indicated by giving names for
the arguments at various positions. This information is also given for
presentation elements in the table of argument requirements in
Section 3.1.3 [Required Arguments], and for content elements in Appendix B [Content Markup Validation Grammar].
ごく少数の要素には、特別な数や種類の引数を必要とするものがあります。
こうした付加的な要請項については、個々の要素とともに述べられています。
A few elements have other requirements on the number or
type of arguments. These additional requirements are described
together with the individual elements.
2.4.4 MathML の属性値
XML 言語使用に依れば、要素に与えられる属性は以下の形式のいずれかをとらねばなりません:
According to the XML language specification, attributes
given to elements must have one of the forms
属性名 = "値"
または
or
属性名 = '値'
ここで、'=' の周りの空白はあってもなくても構いません。
where whitespace around the '=' is optional.
この仕様書では、属性名は一般的に monospace フォントで与えられています。
monospace フォントはマークアップ例でも利用されています。
Attribute names are generally shown in a monospaced font within descriptive text in this
specification, just as the monospaced font is used
for examples.
属性の値は、一般的に MathML では任意の文字列となり得ますが、二重引用符 (") ないし 単引用符 (') のいずれかの組で囲まれていなければなりません。
引用符は、値を囲むものでなければ、文字列の一部として利用することもできます。
An attribute's value, which in general in MathML can be a string of
arbitrary characters, must be surrounded by a pair of either double quotes
(") or single quotes ('). The kind of quotes
not used to surround the value may be included within it.
MathML は、MathML の DTD で必要とされる一般的な XML 属性値よりも複雑な属性値の構文を利用します。
これらの付加的な規則は XML の処理上は必要とされていないものであり、MathML アプリケーションによって利用されることを前提としているものです。従って、この規則に違反することは MathML のエラーになります。
MathML のそれぞれの属性値の構文は、それぞれの要素の説明箇所で、表の形式で以下に示す表記で明記されています。
MathML アプリケーションが属性値を処理する際、各単語や数値を示すための区切り文字として文字と数字の並びを分けるもの以外、空白文字は無視されます。
属性値は、属性についての構文規則に従う限り 第6.2節「MathML で利用する文字」 で挙げられているどんな MathML 文字をも含むことができます。
文字データは属性値に直接含むことができます。つまり、第6.2.1節「Unicode文字データ」で記述されている実体参照が利用できます。
MathML uses a more complicated syntax for attribute values than the
generic XML syntax required by the MathML DTD. These additional rules are
intended for use by MathML applications, and it is a MathML error to
violate them, though they cannot be enforced by XML processing. The MathML
syntax of each attribute value is specified in the table of attributes
provided with the description of each element, using a notation described
below. When MathML applications process attribute values, whitespace
is ignored except to separate letter and digit sequences into
individual words or numbers. Attribute values may contain any MathML
characters listed in Section 6.2 [MathML Characters] permitted by the syntax
restrictions for an attribute. Character data can be
included directly in attribute values, or by using entity references
as described in Section 6.2.1 [Unicode Character Data].
特に、文字 ", ', & と < は、それぞれ ", ', &, < という実体参照を用いて MathML の属性値 (構文規則が許す場合に限り) に含むことができます。
In particular, the characters ", ',
& and < can be included in MathML
attribute values (when permitted by the attribute value syntax) using the
entity references ", ',
& and <, respectively.
MathML DTD は、付録 A「MathML のパース」で与えられていますが、ほとんどの属性値の型を CDATA 文字列として宣言しています。これにより、既存の SGML や XML ソフトウェアとの相互運用性を高め、既にある定義値リストへの追加を可能にします。同様の考察は XML スキーマにも当てはまります。
The MathML DTD provided in Appendix A [Parsing MathML] declares most
attribute value types as CDATA strings. This permits increased
interoperability with existing SGML and XML software and allows extension
to the lists of predefined values. Similar sorts of considerations apply
with XML schemas.
2.4.4.1 MathML 仕様書で利用される構文の表記
MathML で許される独自の属性の構文を記述するために、現文書中のほとんどの属性において以下の規約及び表記が使われます。
To describe the MathML-specific syntax of permissible
attribute values, the following conventions and notations are
used for most attributes in the present document.
| 表記 |
該当するもの |
|
| number |
10進の整数ないし有理数 (一つの小数点を備えた一連の数字)。'-' から始まることもあり得る。 |
| unsigned-number |
10進の整数ないし実数で、符号のないもの |
| integer |
10進の整数、'-'から始まってもよい。 |
| positive-integer |
10進の整数で、符号無し、かつ非0。 |
| string |
任意の文字集合 (必ず完結した属性値となる) |
| character |
一つの空白ではない文字。あるいは MathML の実体参照。空白による区切りがあってもよい。 |
| #rrggbb | RGBの色値。16進の数の組み合わせ。
左からそれぞれ赤、緑、青の割合を x00〜xFF で定義する。
たとえば #5599dd は強いスカイブルーを表す。 |
| h-unit |
水平方向の長さの単位。(許される単位は下で示す) |
| v-unit |
垂直方向の長さの単位。(許される単位は下で示す) |
| css-fontfamily |
下の CSS のサブセクションで説明される。 |
| css-color-name |
下の CSS のサブセクションで説明される。 |
| その他の斜体の単語 |
それぞれの属性で説明されている。ただし、日本語版においては英数字に限る。漢字およびカナに対しては、太字+下線付きで表記される。 |
| form + |
'form' の 1 個以上の存在 |
| form * |
'form' の 0 個ないし 1 個以上の存在 |
| f1 f2 ... fn |
ある形式のものが順番に並ぶ様子。空白文字によって区切られるであろう。 |
| f1 | f2 | ... | fn |
それぞれの形式のうちいずれか。 |
| [ form ] |
'form' の形式があってもなくても良い。 |
| ( form ) |
言い換えると form となりうる。 |
| プレーンテキストの単語 |
その単語そのもの。その単語がそのまま属性値として存在。(ただし、明らかに説明文の一部分ではないときに限る) |
| 引用符付きの記号 |
その記号が、そのまま属性値として存在する (たとえば "+" とか '+') |
構文の表記の中で、演算子の優先順は高い順に以下の通りとなっています:
- form + または form * [最も高い]
- f1 f2 ... fn (形式の並び) [次に高い]
- f1 | f2 | ... | fn (形式の選択) [最も低い]
string は、XML CDATA 属性値で許可されている任意の文字を含むことができます。
MathML 文字に関する議論とその完全な一覧については、第6章「文字、実体とフォント」 を参照してください。
MathML の構文規則には string を属性値の一部としてとることが含まれていません。つまり、文字列は、一つの完全な属性値でなければなりません。
実際の属性値においては、近接したキーワードや数は、number の後で h-unit ないし v-unit のいずれかの構文記号によって表される単位記号を除いて、空白によって区切られなければなりません。
それ以外では、空白文字は必要ではありませんが、上で挙げたトークン間であれば空白があっても構いません。ただし、CSSとの互換性のため、単位記号の直前や、負の数における '-' 記号と数の間、# と rrggbb ないし rgb の間などに空白を置くことはできません。
寸法を表す数値の属性値は、その場でのフォントに依存することが多いので、一般にフォント依存の単位で表すこともできるし、名前付きの絶対的な単位(詳しくは別のセクションで述べてあります)で与えられることもできます。
水平方向の寸法は伝統的に em で与えられ、垂直方向には ex で与えられますが、これらは em ないし ex のいずれかの単位識別子を数値の直後に与えることで指定されます。
たとえば、「+」に代表される演算子の周囲の水平方向の空白は、他の記号が使えるにも拘わらず、伝統的に em で与えられます。
フォント依存の単位は、フォントの大きさの変更に従って大きさを変化させることができるため、絶対的な単位よりも一般に好んで用いられます。
Numerical attribute values for dimensions that should depend upon the current font can be given in font-related units, or in named absolute units (described in a separate subsection below). Horizontal dimensions are conventionally given in em's, and vertical dimensions in ex's, by immediately following a number by one of the unit identifiers em or ex. For example, the horizontal spacing around an operator such as `+' is conventionally given in ems, though other units can be used. Using font-related units is usually preferable to using absolute units, since it allows renderings to grow or shrink in proportion to the current font size.
ほとんどの数値の属性について、表現可能な値のサブセットしか意味を持ちません;
つまり、定義されていない以上はその他の値もエラーではありませんが、レンダラーの判断によって最も近い値に丸められるでしょう。
値として許されるセットはレンダラーに依存し、MathML の定めるものではありません。
For most numerical attributes, only those in a subset of the expressible
values are sensible; values outside this subset are not errors, unless
otherwise specified, but rather are rounded up or down (at the discretion
of the renderer) to the closest value within the allowed subset. The set
of allowed values may depend on the renderer, and is not specified by
MathML.
もし属性値の構文の説明で、たとえば number と integer のように数値が負符号 ('-') を受け付けると書かれている場合、たとえ負の値が意味をなさなくてもそれは構文エラーとはなりません。
その代わり、値はアプリケーションによって前の段落で述べられたように処理されます。
また、構文一覧で指定されていない限り ('+' ないし "+" と引用されている)、正符号 ('+') を数値の一部として明示することができません。また、正符号によって属性値の持つ意味が変わります (正符号を記述できる属性それぞれで説明されています)。
h-unit, v-unit, css-fontfamily および css-color-name などの記号については以降のサブセクションで説明されます。
2.4.4.2 単位を持つ属性
属性によっては、数字の後に「単位識別子」(しばしば「単位」とだけ呼ぶこともあります) を付けたものを、水平の長さや垂直の長さとして受け付けるものもあります。
構文記号 h-unit と v-unit は、それぞれ水平方向の長さと垂直方向の長さを表します。
利用できる単位とその内容に関しては、以下の表に示します;
長さに関して方向による違いはありませんが、属性の構文においては使用される方向に応じて構文記号が区別されます。
単位識別子とその意味は CSS に由来しています。
しかし、CSS においては、数が小数点で終わることはできませんし、'+' 記号で始まっても構いません。
その点で、数の後に単位識別子が並ぶという MathML の構文は、CSS スタイルシートにおける単位付きの長さ値と全く同一ではありません。
MathML で許可されている垂直方向および水平方向の単位は、以下の通りです:
| 単位識別子 |
単位の説明 |
| em |
em (フォント依存の単位で、伝統的に水平方向の長さを表すのに用いられる) |
| ex |
ex (フォント依存の単位で、伝統的に垂直方向の長さを表すのに用いられる) |
| px |
ピクセル、つまり表示上の1ピクセルの大きさ。 |
| in |
インチ (1 インチ = 2.54 センチメートル) |
| cm |
センチメートル |
| mm |
ミリメートル |
| pt |
ポイント (1 ポイント = 1/72 インチ) |
| pc |
ピカ (1 ピカ = 12 ポイント) |
| % |
標準値に対する百分率 |
植字の単位である em および ex については、付録 H「用語集」 で定義されています。また、以下の「注釈」でも議論されています。
% は「相対的な単位」です;
属性値が n% (n は任意の数値) の形式で与えられる場合、その値は標準の値に n をかけて 100 で割ったものとして与えられます。
標準の値 (非定数の場合はその状況に合わせて得られるべき値) はそれぞれの要素に対する属性の表の中に掲出されています。また、その意味はその属性についての下位の文書で説明されています。
(なお、mpadded 要素は % についての独自の構文をもち、単位識別子としての % が認められません。)
CSSとの一貫性を保つため、MathML における長さの単位は、ほとんどの場合において省略できません。
省略できるものについては、属性値の構文では単位記号は数値の後に角括弧で囲まれています (たとえば 数値 [ h-unit ] のように )。
単位を明記しない場合の挙動については、それぞれの属性についての文書で示されていますが、一般的には属性のデフォルト値の何倍であるかを示します。
(単位なしの数 nnn は、nnn の100倍に % を漬けたものと等価です。たとえば、<mo maxsize="2">(</mo> は <mo maxsize="200%">(</mo> と等価です。)
特別な例外として (これもまた CSS と同様に)、上の構文で単位が必要なものについても、数値 0 は単位識別子をつける必要がありません。
このような場合では、単位識別子はなんでも構いません。なぜなら、どんな単位でも 0 は 0 だからです。
多くの属性に対して、典型的な単位は植字において使われるもので、この仕様書でもデフォルト値の単位として用いています。
特にデフォルト値が示されていない場合でも、典型的な単位は構文表か属性についてのそれぞれの説明の中で与えられています。
ほとんどの共通単位は em か、あるいは ex です。しかし、特殊な属性値をのぞけば、どんな単位も使うことができます。
単位に関する補足
属性によっては、一つ以上の数値を含み、それらには別々の単位が付くことがあり得るという点に注意してください。 (たとえば <mtable> の framespacing 属性)
慣例では、主に垂直長さにはフォント依存の単位 ex を、水平長さには単位 em を使いますが、これらは必要条件ではありません。
これらの単位は、その属性値が定義しようとする要素のレンダリングに用いられるフォントとそのサイズに依存するものであり、従って同一要素内に fontfamily や fontsize のような属性が同時に現れる場合は、その あとに 解釈されなければなりません。というのも、表示フォントやそのサイズを変更することにより、これらの単位での長さが変わってしまうからです。
それぞれの単位の長さの定義 (ただし MathML の長さを表現する構文は除きます)
は、CSS によって明示されます。なお、CSS によって定義される値 (フォントサイズおよび 'x' の文字高さ) と異なる別の em 値および ex 値をフォントがもつ場合については、例外的にフォントによって定められる値が用いられるべきです。
2.4.4.3 CSS と互換性のある属性
MathML の属性には、[CSS1] でもともと定義されているテキストの描画プロパティに非常によく対応した物 (以下に挙げます) があります。
MathML 1.01 では、これらの属性の名前と値は、可能な限り CSS 勧告に対応させていました。これは、属性のデフォルト値を決定する際に、CSS 環境のレンダラーが対応するプロパティを検索しやすくするためです。
スタイルプロパティを MathML の属性経由と、CSS スタイルシート経由の両方で設定できるようにすることには、難点があります。
まず紛らわしいということ、そして最悪なのは、文書全体に及ぶCSSの不注意な変更で数式の意味が変わってしまうことです。この理由から、これらの属性は 廃止されました。
その代わりに、MathML 2.0 では、4つの新しい数学スタイル属性を導入しました。
These attributes use logical values to better capture the
abstract categories of letter-like symbols used in math, and afford a
much cleaner separation between MathML and CSS.
詳しくは、第3.2.2節「トークン要素に共通な数学用スタイル属性」を参照してください。
参考のために、以下の表では廃止された MathML 1.01 のスタイル属性と CSS との対応を示します:
class, style, id 属性のスタイルシートとの併用についての議論は、下の 第2.4.5節「MathML 要素が共有する属性」もご覧下さい。
属性値の処理順のスタイルシートとの比較
CSS or analogous style sheets can specify changes to rendering
properties of selected MathML elements. Since rendering properties
can also changed by attributes on an element, or changed automatically
by the renderer, it is necessary to specify the order in which changes
from various sources occur. An example of automatic adjustment is what
happens for fontsize, as explained in the
discussion on scriptlevel in Section 3.3.4 [Style Change (mstyle)]. In the case of `absolute' changes,
i.e., setting a new property value independent of the old value (as
opposed to `relative' changes, such as increments or
multiplications by a factor), the absolute change performed last will
be the only absolute change which is effective, so the sources of
changes which should have the highest priority must be processed
last.
In the case of CSS, the order of processing of changes
from various sources which affect one MathML element's
rendering properties should be as follows:
(first changes; lowest priority)
-
Automatic changes to properties or attributes based on the type of the
parent element, and this element's position in the parent, as for the
changes to
fontsize in relation to scriptlevel mentioned above; such changes will usually
be implemented by the parent element itself before it passes a set of
rendering properties to this element
-
From a style sheet from the reader: styles which are not
declared `important'
-
Explicit attribute settings on this MathML element
-
From a style sheet from the author: styles which are not
declared `important'
-
From a style sheet from the author: styles which are
declared `important'
-
From a style sheet from the reader: styles which are
declared `important'
(last changes; highest priority)
Note that the order of the changes derived from CSS style sheets is
specified by CSS itself (this is the order specified by CSS2).
The following rationale is related only to the
issue of where in this pre-existing order the changes caused by explicit
MathML attribute settings should be inserted.
Rationale: MathML rendering attributes are analogous to HTML rendering
attributes such as align, which the CSS section on
cascading order specifies should be processed with the same priority.
Furthermore, this choice of priority permits readers, by declaring certain
CSS styles as `important', to decide which of their style
preferences should override explicit attribute settings in MathML. Since
MathML expressions, whether composed of `presentation' or
`content' elements, are primarily intended to convey meaning,
with their `graphic design' (if any) intended mainly to aid in
that purpose but not to be essential in it, it is likely that readers will
often want their own style preferences to have priority; the main exception
will be when a rendering attribute is intended to alter the meaning
conveyed by an expression, which is generally discouraged in the
presentation attributes of MathML.
2.4.4.4 属性のデフォルト値
一般に MathML 属性のデフォルト値は、それぞれの要素に対して詳細な記述とともに与えられています。明らかな説明文がなければ、要素の属性表の中でプレーンテキストで示されるデフォルト値は文字通り適用されるものであり、斜体 (この訳文中の日本語文字では下線付きの太字) で示されるものはデフォルト値がどのように計算されるかについての説明です。
継承と書かれたデフォルト値は描画環境から引き継がれるもので、mstyle をはじめとする要素 (それぞれ説明されています) について、他の周辺要素の属性値の一部または全部から値を得るものです。
The value used will always be one which could have been specified
explicitly, had it been known; it will never depend on the content or
attributes of the same element, only on its environment. (What it means
when used may, however, depend on those attributes or the content.)
Default values described as automatic should be computed by
a MathML renderer in a way which will produce a high-quality rendering; how
to do this is not usually specified by the MathML specification. The value
computed will always be one which could have been specified explicitly, had
it been known, but it will usually depend on the element content and
possibly on the rendering environment.
Other italicized descriptions of default values which appear in the
tables of attributes are explained for each attribute individually.
The single or double quotes which are required around attribute values
in an XML start tag are not shown in the tables of attribute value syntax
for each element, but are shown around example attribute values in the
text.
Note that, in general, there is no value which can be given explicitly
for a MathML attribute which will simulate the effect of not specifying the
attribute at all for attributes which are inherited or
automatic. Giving the words `inherited' or
`automatic' explicitly will not work, and is not generally
allowed. Furthermore, even for presentation attributes for which a
specific default value is documented here, the mstyle element (Section 3.3.4 [Style Change (mstyle)]) can be
used to change this for the elements it contains. Therefore, the MathML DTD
declares most presentation attribute default values as #IMPLIED,
which prevents XML preprocessors from adding them with any specific default
value. This point of view is carried through to the MathML schema.
2.4.4.5 MathML DTD 中の属性値
XML の DTD では、属性値を一般的な文字列として宣言することもできますが、とりうる値を列挙したり特別なデータ型として宣言することで、そのデータ型を制限することができます。
XML 属性の型の選択は、DTDを利用する正当性の検査を行える範囲に影響します。
MathML の DTD は、すべての MathML 属性に対して、値の列挙も含め、XML 属性型を正しく指定しています。
しかし一般的に、MathML の DTD は比較的寛容で、属性値を文字列として宣言していることも少なくありません;
これは、SGML パーサーとの相互運用性を提供することを目的としたもので、一つの MathML 要素の複数の属性が同じ値をとる (たとえば true と false) ことや、定義済みの値の一覧の拡張が許容されるようになっています。
また、既に述べたように (そしてこの後でも述べられていますが)、DTD で属性値が文字列として宣言されていても、MathML では特定の値しか許可されない場合があります。
たとえば、多くの属性は数値であることが期待されています。
許される属性値については、それぞれの要素ごとにこの後のセクションで説明されています。
これらの制限事項が、実際に MathML によるものなのか判断するためには、付録 A「MathML のパース」を参照して下さい。
ただし、DTD の制限が緩いからといって、制限事項が MathML 言語の一部ではないとか、あるいは MathML のレンダラーに依存するということではありません。
(MathML のエラーにレンダラーがどのように対応すべきかについては、第7.2.2節「エラー処理」を参照してください。)
なお、MathML DTD は便宜上提供されているものです;
たとえこの仕様書と同じ事を意図してあるとしても、相違があった場合はこの仕様書の文章が絶対的に正しいのです。
(この仕様書の多くの章の間に存在しうる相違は、第6章「文字、実体とフォント」をまず読んだ上で、第3章「プレゼンテーション・マークアップ」、第4章「コンテンツ・マークアップ」、第2.4節「MathMLの構文と文法」そして残りの文章を読むことで解決するはずです。)
MathML のスキーマについても同様です:
公開されている勧告の文書が優先されるのです。
もちろん、実用上困難であることは、予め予想されています。
DTD やスキーマをベースとした検査パーサーを利用する以上、MathML を処理するシステムでは、それが仕様書を完全に満たすものであっても、不正な構文として扱われる箇所を検出して、処理を停止する可能性があります。
2.4.5 すべての MathML 要素に共通な属性
[XSLT] や [CSS2] などのスタイルシートのメカニズムの利用を可能にするために、すべての MathML 要素はそれぞれの要素で明示的に示される属性に加えて、class 属性、style 属性、および id 属性を受け付けます。
CSS をサポートしない MathML のレンダラーは、これらの属性を無視することがあります。
スタイルシートではもっと限定的な構文を採用されていますが、MathML ではこれらの属性値を一般的な文字列と指定しています。
つまり、これらの属性値に対しては、MathML ではどんな値でも有効です。
また、リンクのメカニズムとの互換性を利用するために、すべての MathML 要素は xlink:href 属性を受け付けます。
平行マークアップ (第5.3節「平行マークアップ」) で利用するために、すべての MathML 要素は xref 属性も受け付けます。
同じ理由により、id も利用できます。
MathML 1.0 との下位互換性のために、すべての MathML 要素は 推奨されない 属性のうち、MathML の DTD に違反することなく非標準の属性を受け付けさせるために考案された other 属性も受け付けます (第7.2.3節 [Attributes for unspecified data])。
MathML のレンダラーは、この属性が MathML の標準属性ではないときに限りこの属性を処理します。
しかし、MathML では特定の情報を処理させるための別の方法がすでに用意されていますので、other の使用は全く推奨されません。
多くのプレゼンテーション・マークアップのトークン要素で利用できる MathML の属性については、第3.2.2節「トークン要素に共通な数学スタイル属性」 を参照してください。
2.4.6 省略される空白の処理
MathML では、トークン要素の外にある空白は無視されます。
また、トークン要素の外の空白以外の文字は許可されません。
トークン要素の本体にある空白は、前後から削除されます。
つまり、本体の前後の空白はすべて削除されます。
MathML 要素の本体の中に含まれる空白は畳み込まれて正規化されます。
つまり、1つ以上の空白文字の連続は、1つの空白文字 (いわゆるブランク文字) に置き換えられるのです。
XML と同様、MathML では「空白」はスペース(SP)、タブ(TAB)、改行(LF)、復帰(CR)のことを指します。
これらは16進の Unicode コードでそれぞれ U+0020, U+0009, U+000A, U+000D に該当します。
たとえば、<mo> ( </mo> は <mo>(</mo> と等価ですし、
<mtext>
定理
1:
</mtext>
は
<mtext>定理 1:</mtext>
と全く同じ意味をもちます。
トークンの最初や最後で空白文字を追加したい時や、一つ以上の空白を無視せずに符号化したい時は、 や、第6.2.4節「非マーキング文字」で述べられている他の「空白」非マーキング実体を使用する必要があります。
たとえば、以下の2つのマーキングを比較してください:
<mtext>
定理
1:
</mtext>
および
<mtext>
定理 1:
</mtext>
1つ目の例が描画される際には、「定理」の前には空白はなく、「定理」と「1:」の間には1つの空白があり、「1:」の後には空白はありません。
2つ目の例では、「定理」の前には1つの空白があり、「定理」と「1:」の間には2つの空白が、そして「1:」の後には空白がありません。
XML プロセッサーはトークン中の空白を MathML プロセッサにそのまま渡すため、xml:space 属性がこの状況では適用されないことに注意してください; 空白文字は MathML の規則に従って削除されたり畳み込まれたりするのです。
トークン要素である mi, mn, mo, ms, mtext, ci, cn および annotation の外の空白に対しては、「空白」実体だけ含む mtext 要素ではなく、mspace 要素を使うべきです。
概要: 数学用マークアップ言語 (MathML) バージョン 2.0
前: 1 導入
次: 3 プレゼンテーション・マークアップ
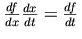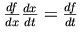
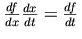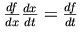 .
.
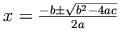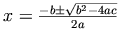 .
.![A=\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]](image/f2008.gif) .
.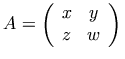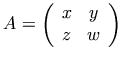 .
.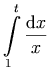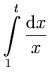 .
.