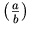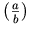 as opposed to the default rendering
as opposed to the default rendering
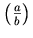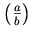 .
.
概要: 数学用マークアップ言語 (MathML) バージョン 2.0
前: 2 MathML の基礎
次: 4 コンテンツ・マークアップ
3 プレゼンテーション・マークアップ
3.1 導入
3.1.1 プレゼンテーション・マークアップで表現できるもの
3.1.2 この章で使用する用語
3.1.3 必要な引数
3.1.4 扱いが特殊な要素
3.1.5 双方向レイアウト
3.1.6 プレゼンテーション要素のまとめ
3.2 トークン要素
3.2.1 トークン要素における MathML 文字
3.2.2 トークン要素に共通な数学用スタイル属性
3.2.3 識別子 (mi)
3.2.4 数 (mn)
3.2.5 演算子、囲い文字、区切り文字、アクセント (mo)
3.2.6 Text (mtext)
3.2.7 Space (mspace)
3.2.8 String Literal (ms)
3.2.9 Adding new character glyphs to MathML
(mglyph)
3.3 General Layout Schemata
3.3.1 Horizontally Group Sub-Expressions
(mrow)
3.3.2 Fractions (mfrac)
3.3.3 Radicals (msqrt, mroot)
3.3.4 Style Change (mstyle)
3.3.5 Error Message (merror)
3.3.6 Adjust Space Around Content
(mpadded)
3.3.7 Making Sub-Expressions Invisible (mphantom)
3.3.8 Expression Inside Pair of Fences
(mfenced)
3.3.9 Enclose Expression Inside Notation
(menclose)
3.4 Script and Limit Schemata
3.4.1 Subscript (msub)
3.4.2 Superscript (msup)
3.4.3 Subscript-superscript Pair (msubsup)
3.4.4 Underscript (munder)
3.4.5 Overscript (mover)
3.4.6 Underscript-overscript Pair
(munderover)
3.4.7 Prescripts and Tensor Indices
(mmultiscripts)
3.5 Tables and Matrices
3.5.1 Table or Matrix
(mtable)
3.5.2 Row in Table or Matrix (mtr)
3.5.3 Labeled Row in Table or Matrix
(mlabeledtr)
3.5.4 Entry in Table or Matrix (mtd)
3.5.5 Alignment Markers
3.6 Enlivening Expressions
3.6.1 Bind Action to Sub-Expression (maction)
この章では、MathML の「プレゼンテーション」要素について定めています。 プレゼンテーション要素は、数学的な記法のレイアウト上の構造について記述することができます。
プレゼンテーション要素は、従来の数学表記における「コンストラクター」に対応します。つまり、従来の数学表記の中ですべての数式を構成する、記号と式による基本的な構造に対応しています。 従来の視覚上の表記は非常に大切ですから、ここで出てくる要素が表す表記上の構造については、視覚的な言葉で説明されます。 ただし、音声発話装置にも十分な情報を含むように設計されているという点では、要素は視覚的な構造に完全に従属しているわけではありません。 これらの要素の属性の中は、視覚的なメディアでしか意味をなさないものもありますが、ほとんどの属性は音声メディアでも同様の方法で扱うことができます (たとえば、時間的な「間」と水平方向の間隔を対応づけることによって)。
メディア依存のレンダリングや各自のスタイルの好みを可能にするため、MathML のプレゼンテーション要素はレンダリングの方法を示唆しているに過ぎません (つまり、必須ではありません)。 この仕様書では、視覚的なレンダリング規則を詳細に提案するところがありますが、しかし MathML レンダラーはわかりやすければ独自の規則を利用して構いません。
表題・セクション・段落がテキスト文書の高度な構文構造を表現するのと同様に、プレゼンテーション要素は式の構文構造を表現します。
従って、たとえば「x + a / b」のような変数と演算子の列も、必ずしもただ一つの mrow 要素 (引数を水平方向の列としてレンダリングする要素) によって表されるのではなく、式を構成する入れ子式の副式にそれぞれ対応した複数の mrow 要素によって表されます。
つまり、この場合は下のようになります:
<mrow>
<mi> x </mi>
<mo> + </mo>
<mrow>
<mi> a </mi>
<mo> / </mo>
<mi> b </mi>
</mrow>
</mrow>
また、上付文字は、先行する単一の文字に付くのではなく、基底を構成する式全体に対して付きます。 この構造によって、文書制作者が表示幅などのレンダリング環境の詳細を把握できない時でも、より高画質な数学のレンダリングが可能となります。 また、表現された数学構造の機械的に解釈することも容易になります。
MathML の文字の中には、演算子や変数の名前に用いられる物があり、従来の数学表記の中で他の記号 ⅆ や ⅇ や ⅈ のような記号や、⁢ や ⁡ や ⁣ のように不可視な演算子と同様にレンダリングされていました。
これらは、それぞれ別の読み上げられ方をしたり、改行や空白の効果が異なる場合があるので、表記上の別々な記号やオブジェクトだと考えられ、従って、特別な実体参照によって適切に表現されるべきです。
たとえば、視覚的に「f(x)'」と表現される式は、英語では一般に、単に「f x」ではなく「f of x」と読まれます;
これは MathML では ⁡ 演算子を「f」の後に用いることで表現可能で、この場合音声では「of」とレンダリングされるでしょう。
MathML の実体の完全なリストは 第6章「文字、実体とフォント」 で説明されています。
この章を読む前に、MathML の構文と文法について 第2.4節「MathML の構文と文法」 を読むことを強く推奨します。 この第2.4節は、MathML の表記と規約について重要な情報を含んでいます。 この第3章では特に、読者が基本的な XML 用語について 第2.4.2節「XML 構文入門」を、属性値の表記と規約について述べられている 第2.4.4節「MathML の属性値」を、それぞれ読んでいることを前提としています。
この節の残りでは、この章で使用する MathML 独自の用語と規約について紹介しています。
プレゼンテーション要素は大きく 2 種類に分類することができます。
トークン要素は個々の記号、名前、数、ラベルなどを表現するものです。
トークン要素は、一般に、文字のみを本体として含むことができますが、例外として、垂直方向の位置揃えを表現する malignmark 要素、mglyph 要素と、実体参照があります。
レイアウトスキーマは、数式の部品をまとめて大きな数式に構成するもので、空白 (無視される) を除いては要素のみを本体として含みます。
その他に、他のレイアウトスキーマと共に用いられる空要素があります。
式中の個々の「記号」は MathML のトークン要素によって表現されます。
基本的な MathML のトークン要素は、識別子 (たとえば変数や関数名)、数、演算子 (括弧のような囲い文字や、カンマのような区切りも含む) を表すものです。
数学的な重要性というよりは審美的な重要性のためにテキストや空白を表現するトークン要素もありますし、自動数式システムとの互換性を持たせるために「文字列リテラル」を表現する要素もあります。
ただし、トークン要素は単一で意味を持つ「記号」(名前、数、ラベル、数学記号など) を表現するとは要っても、その記号が 1 つ以上の文字から成り立つことがあるということに注意して下さい。
たとえば、sin と 24 は、単一のトークン要素によって、それぞれ <mi>sin</mi> や <mi>24</mi> と表現されます。
従来の数学表記では、式は副式から再帰的に構築され、究極的には一つ一つの記号から構成されていました。 それぞれのパーツは、表記上の構造の小さな集合をグループ化ないし配置してできていました。 この方法は、「式のコンストラクター」として考えることができます。 MathML でも、式は同様に構築され、レイアウトスキーマが副式から式を構成する方法を指定します。 ここでは、従来の数学の植字において副式から式を形成していたレイアウト方法と、それぞれのレイアウトスキーマを対応づけて、用語が導入されています。
この章で出てくる特殊な要素、そして要素間の関係は、以下の通り: プレゼンテーション要素 は、MathML の要素で、この章で定義するものです。 この要素は 第3.1.6節「プレゼンテーション要素のサマリー」 に一覧を挙げています。 コンテンツ要素 は、MathML の要素で、第4章「コンテンツ・マークアップ」 で定義しています。 コンテンツ要素は、第4.4節「コンテンツ・マークアップ要素」 に一覧があります。
MathML の 式(expression) とは、空要素 none や mprescripts のような例外を含む、プレゼンテーション要素の単一のインスタンス、あるいは、プレゼンテーション要素の本体として許されているコンテンツ要素 (これについては 第5.2.4章「プレゼンテーション・マークアップ中のコンテンツ・マークアップ」 で述べられています) の単一のインスタンスです。
式 E の 副式(sub-expression) とは、E の本体の一部を構成するすべての MathML の表現のことで、それは 直接的 あるいは 間接的、すなわちそれが E の「子」であるかどうかに依りません。
レイアウト・スキーマは、その子の数や位置に特別な意味を与えますので、レイアウト・スキーマの子も要素の 引数 と呼ばれます。 上記のように定義した結果として、レイアウト・スキーマの本体には、その子となる0個以上の要素の列が含まれることになります。
ここで説明する要素のほとんどは、特定の数の引数 (常に 1, 2, ないし 3) を必要とします。 下にある要素の構文に関しての詳しい説明の中では、必要とされる引数の数は引数の位置や名前から暗に知ることができます。 引数の数や種類にそれ以上の要請をする要素はそれほど多くはありません (それぞれの要素について説明されています) 。 0 個以上の引数を受け付ける要素がありますが、それは、全く引数が無くても構わないということです。
空白を描画するための MathML の要素が、含まれる要素の引数として見なされることに注意してください。
このような空白を扱う要素の正しい利用法については、第3.2.7節「空白 (mspace)」 を参照してください。
mrow下の表に挙げた要素で、必要な引数が 1* とされているもの (msqrt, mstyle, merror, menclose, mpadded, mphantom, mtd と math) は、実際には引数がいくつあっても構いません。
しかし、引数が 0 個の時、あるいは 1 個より多い時 (i.e. 2個以上の時)、その引数すべてから形成される mrow 要素を一つ含むものと推定 (inferred) して扱われます。
なお、math 要素はプレゼンテーション要素ではありませんが、下の一覧では完全を期すために追加されています。
たとえば
<mtd> </mtd>
というコードは、以下のように扱われます:
<mtd> <mrow> </mrow> </mtd>
また、
<msqrt> <mo> - </mo> <mn> 1 </mn> </msqrt>
というコードは、以下のようになります:
<msqrt>
<mrow>
<mo> - </mo>
<mn> 1 </mn>
</mrow>
</msqrt>
この機能のおかげで、MathML データは多くの mrow 要素を含む必要が無く、データ制作者は本来必要なこの要素を省略することができるのです。
レンダリングの方法を考える際、上で挙げた要素については、この方法で引数全体から形成される mrow 要素をただ一つの式として本体に持つ、と考えることができます。
ただし、これらの要素は、通常は一つの式を処理する考えられるので、下の表では引数の数は 1* と記述してあります。
ここで、便利のために、それぞれの要素で必要な引数の数を表に纏めてあります。
それぞれの引数の役割が決まっている場合は、その役割も書いてあります。
引数の数が 1* となっているものは、既に述べたように mrow 要素を推定するということを意味しています。
| 要素 | 必要な引数の数 | 引数の意味 (位置によって意味が変わる場合) |
|---|---|---|
mrow |
0 以上 | |
mfrac |
2 | 分子 分母 |
msqrt |
1* | |
mroot |
2 | 基底 index |
mstyle |
1* | |
merror |
1* | |
mpadded |
1* | |
mphantom |
1* | |
mfenced |
0 以上 | |
menclose |
1* | |
msub |
2 | 基底 下付き文字 |
msup |
2 | 基底 上付文字 |
msubsup |
3 | 基底 下付文字 上付文字 |
munder |
2 | 基底 下ルビ (underscript) |
mover |
2 | 基底 上ルビ (overscript) |
munderover |
3 | 基底 下ルビ 上ルビ |
mmultiscripts |
1 以上 | base
(subscript superscript)*
[<mprescripts/>
(presubscript presuperscript)*] |
mtable |
0 or more rows | 0 個以上の mtr 要素または mlabeledtr 要素 |
mlabeledtr |
1 以上 | ラベルと 0 個以上の mtd 要素 |
mtr |
0 以上 | 0 個以上の mtd 要素 |
mtd |
1* | |
maction |
1 以上 | actiontype 属性に依存 |
math |
1* |
MathML のプレゼンテーション要素の中には、文脈によっては特別な役目を果たすものがあります。 そういった特別な動作については、下の詳しい要素の説明の中で述べていますが、 便利のために、ここで特別な動作のうち重要な種類について挙げておきます。
要素の中には空白と考えて良いものがあり、第3.2.7節「空白 (mspace)」 で定義されています。
この定義は、mo 要素 (第3.2.5節「演算子、囲い文字、区切り文字、アクセント (mo)」) についてのレンダリング規則に影響があります。
msup のような要素では、1番目の引数となる演算子を修飾することができます。
このような要素は 第3.2.5節「演算子、囲い文字、区切り、アクセント (mo)」 に一覧で挙げ、明確に「修飾される演算子」(embellished operator)を定義し、これが伸縮可能な演算子のレンダリング規則にどう影響するか説明しています。
要素の中には、1つ以上の引数を指定すると、その引数を「推定の mrow」(inferred mrow) の引数とみなすものがあります。
これについては 第3.1.3節「必要な引数」 を参照してください。
MathML 1.x では、mtable 要素は mtr 要素をその引数の親として推定し、mtr 要素は mtd 要素をその引数の親として推定していました。
MathML 2.0 では、mtr 要素と mtd 要素は必ず明示的に書かねばなりません。
ただし、過去との互換性のため、レンダラーは mtr 要素と mtd 要素を推定することが望まれます。
「双方向レイアウト」という用語は、アラビア語やヘブライ語のような一部の言語では文字が右から左に向かって書かれ、これらの言語の中に左から右に向かって書かれた数字やアルファベットを混ぜると 1 つの行ないし段落の中に 2 種類の方向が生じてしまうという状況を示しています。
一般的なテキストに関して言えば、Unicode の仕様によって双方向アルゴリズムが定められています [Bidi]。 このアルゴリズムは、「バッキングストア」(訳注: バッファの一種) 中の文字の順番が論理順序 (つまり、発音ないしタイプされる順) にあるとみなし、 文字属性や他のディレクティブに従って表示の際に文字がどのように記録されるかを決定します。 HTML, CSS, XSL, SVG ではこのアルゴリズムを採用し、マークアップやスタイルシートによって表示順を制御します。
数式中の双方向レイアウトは、テキスト中のそれに比べてより複雑になります。 これは、数学のレイアウトが2次元的な性質を持っていることや、 空間的な位置関係で表記の意味を伝えることが原因です。 また、右から左へ書く言語の中でもあまり双方向レイアウトを利用しないため、 双方的なレイアウトに関する約束事が確立していないことも原因となっています。
こうした状況を踏まえ、MathML 2.0 では Unicode 双方向アルゴリズムのうち、 限られたもののみを採用しました。 この節の残りでは、このアルゴリズムについて説明します。
MathML のテキストを含むことができるトークン要素 (mtext, mo, mi, mn and ms) では、
その内容が視覚的にレンダリングされる際には Unicode 双方向アルゴリズムの implicit part が採用されます (つまり文字属性に基づいて並べ替えられます) [Bidi]。
ここで、基本となる方向は left-to-right です。
Unicode 双方向アルゴリズムの implicit part は、1文字のみしかない場合や、right-to-left の指向性の強い文字 (つまりアラビア語やヘブライ語などの文字) がない場合、left-to-right レイアウトと同一です。
right-to-left の指向性の強い文字をレンダリングする必要がない場合、 アプリケーションは Unicode 双方向アルゴリズムの適用が要請されません。
超限濃度 (transfinite cardinal) を表現するヘブライ文字に、コード番号 U+2135 から U+2138 (ALEF SYMBOL, BET SYMBOL, GIMEL SYMBOL, DALET SYMBOL) が使われることに注意してください。 これらは、左から右への強い指向性を持ちます。
MathML 2.0 は、数式において、右から左へ記述するレイアウトや、 双方向レイアウトについては扱っていません。 サポートされるのは、左から右へのレイアウトのみです。 数式の右から左へのレイアウトについては、 MathML の将来的なバージョンで扱われることでしょう。
mi |
識別子 |
mn |
数 |
mo |
演算子、囲い文字、区切り文字 |
mtext |
テキスト |
mspace |
空白 |
ms |
文字列リテラル |
mglyph |
MathML に新しい文字グリフを加える |
mrow |
任意の数の副式を水平方向にグループ化する |
mfrac |
2つの副式から1つの分数を作成する |
msqrt |
2乗根を作る (radical without an index) |
mroot |
form a radical with specified index |
mstyle |
スタイルを変更する |
merror |
プリプロセッサからの構文エラーメッセージを enclose する |
mpadded |
本体の周囲の空白を調整する |
mphantom |
場所を確保し、しかし本体を不可視にする |
mfenced |
1対の囲い文字で本体を囲む |
menclose |
enclose content with a stretching symbol such as a long division sign. |
msub |
下付き文字を設定する |
msup |
上付文字を設定する |
msubsup |
下付・上付文字の組を設定する |
munder |
下ルビ(underscript)を設定する |
mover |
上ルビ(overscript)を設定する |
munderover |
下ルビ・上ルビの組を設定する |
mmultiscripts |
attach prescripts and tensor indices to a base |
mtable |
表、あるいは行列 |
mlabeledtr |
表ないし行列のラベルや式番号のついた行 |
mtr |
表ないし行列の行 |
mtd |
表ないし行列の1つのエントリー |
maligngroup および
malignmark |
字寄せのマーカー |
maction |
bind actions to a sub-expression |
プレゼンテーション・マークアップにおけるトークン要素は、 数学表記の最小の単位に対応し、意味を伝えるためのものです。 トークンとは、テキストにおける単語に類似していると言えます。 しかし、数学表記は正確かつ記号的な性質を持っているため、 テキストデータでは個々の単語を特別にマークアップしたりスタイルを付けたりする必要はありませんが、 MathML マークアップにおいてはトークン要素の種類やプロパティがとても重要です。
トークンは、一般に一つの数学記号を表現する単一の文字から構成されますが、 その他にも、関数名など、複数の文字からなるトークンもあります。 さらに、従来の数学表記では植字上のプロパティによって記号を区別して使ってきた (e.g. リー代数には Fraktur 書体の 'g' を用いたり、ベクトルの表記には太字の 'x' を用いたりします) ので、スタイル・メカニズムが植字上のプロパティを遵守して意味が損なわれないように注意しなければなりません。 従って MathML においては、文字、トークン、記号の植字上のプロパティは、 それぞれ密接な関係があります。
MathML マークアップの中では、文字データはトークン要素の本体としてのみ存在できます。
唯一の例外は、要素間のホワイトスペースで、これは無視されます。
トークン要素は、任意の 0個以上の Unicode 文字列を含むことができます。
特に、本体が空のトークンが許されており、一般には不可視に、つまり通常のトークン要素の周囲の空白以外に幅を持たずに、描画する際に用います。
空要素 mspace と mglyph は、この限りではありません。
mspace 要素の幅は、属性値に依存しています。
mglyph 要素は、その属性が表現する文字を用いて描画します。
すべての Unicode 文字データはトークン要素の本体として有効ですが、
MathML 2.0 は、名前突きの Unicode 3.2 文字からなる特別なサブセットを区別し、
これを文書中で〈MathML 文字〉と呼んでいます。
MathML 文字の完全な一覧は、第6章「文字、実体とフォント」 で定義しています。
MathML 文字は、直接 Unicode 文字データで表現されることもありますし、
数値文字参照ないし文字実体参照の形で間接的に表現されることもあります。
数値文字参照と文字実体参照の利点と欠点についての議論に関しては、第6章「文字、実体とフォント」 を参照してください。
新しい数学用の文字、つまり既存の MathML 文字の非標準的なグリフは、mglyph 要素によって表現されます。
mglyph 要素以外には、malignmark 要素がそれ以外で唯一トークンの本体として認められます。
詳しくは 第3.5.5節「アラインメント・マーカー」 を参照してください。
mspace および mglyph 以外のトークン要素は、
この2要素の本体としてレンダリングされるべき
(i.e. 視覚的な場合で言えば、本体における文字中で、
密接した標準的なグリフの水平方向の列として描画されるべき)
です。
レンダリングのアルゴリズムは、
後述の数学スタイル属性によって実現されるべきで、
それぞれのトークン要素の種類によって異なる規則ないし属性によって
周囲の空白を調整するべきです。
数学で用いられる記号の大部分は、1文字の識別子で、 主に数式中で変数名として使われます。 異なった書体の文字は、それぞれ異なった記号として扱われます。 たとえば、Fraktur書体の 'g' という記号はリー代数を表し、 ローマン体での 'g' は、それに対応する リー群を表します。 このような文字主体の記号は、字間や線種など、 テキスト本文中の文字とは変えて植字されます。 どんな些細なスタイルの変換でも数式中における意味を変えてしまうおそれがあるため、 これらの文字のスタイル・メカニズムは特別に扱う必要があります。
このような理由から、Unicode 3.1 では、900以上もの数学用の記号文字が導入されました。 この新しい文字は、SMP (Secondary Multilingual Plane) に格納されています。 詳しくは、第6章「文字、実体、フォント」 を参照してください。 MathML 2.0 で許容される文字は、この正式な Unicode データですので、ツールやフォントが広く利用されるようになります。私たちは、これこそが文字用の記号を記述する最も優れた方法だと考えています。
SMP文字のサポートは広く用いられるでしょう。しかし、マークアップによって BMP (Basic Multilingual Plane) 文字のみを使う代替的なエンコーディングもまた提供される必要があります。
MathML 2.0 では、BMP 文字データの組み合わせによるトークン要素、mathvariant属性、そして SMP Math Alphanumeric Symbol 文字を含むトークンの間の対応付けを定義しています。
SMP 文字を受け付けるプロセッサー・アプリケーションは、対応するBMPや属性の組み合わせも同様に扱わねばなりません。
次の節では mathvariant 属性についてより詳しく述べています。また、完全な技術説明は 第6.2.3節「数学用英数字記号の文字」 で提供されています。
MathML 2.0 には、新しく4つの 数学用スタイル mathematics style 属性が導入されました。
これらの属性は、mspace と mglyph を除くすべてのプレゼンテーショントークン要素で有効です。これは mstyle 要素も例外ではありません。
4つの属性は以下の通りです:
| 名前 | 値 | 標準値 |
|---|---|---|
| mathvariant | normal | bold | italic | bold-italic | double-struck | bold-fraktur | script | bold-script | fraktur | sans-serif | bold-sans-serif | sans-serif-italic | sans-serif-bold-italic | monospace | normal (<mi>は除く) |
| mathsize | small | normal | big | number v-unit | 継承される |
| mathcolor | #rgb | #rrggbb | html-color-name | 継承される |
| mathbackground | #rgb | #rrggbb | html-color-name | 継承される |
(属性値の表記についての用語と表記については、第2.4.4節「MathML 属性値」 を参照のこと)
数学用スタイル属性では、トークン要素の論理クラスが定められます。 それぞれのクラスは、与えられた数式の中で意味を持つ印刷関係の記号トークンの集合に対応させるするものです。 従って、他のスタイルとは視覚的に区別され、文書全体のスタイルの変更によってうっかり意味が変わってしまうことがないよう保護される必要があります。
CSS が利用できる環境で MathML がレンダリングされる際、 数学用スタイル属性はCSSスタイル規則用のあらかじめ定められたセレクターとして 見ることができます。 より詳しい議論とCSSスタイルシートの例については、第7.1.5節「CSSとMathMLの共用」 および 付録G「MathML用CSSスタイルシートの例」 を参照してください。 CSS が利用できない場合、他の論理クラスとの視覚的な区別は、描画アプリケーション内部のスタイル機構に依存します。
理論的には、レンダラーは数学用のスタイル属性と特定の描画プロパティとのマッピングを自由に行うことができます。しかしながら、実際には、数学用スタイル属性名とその値は、植字上のプロパティを示唆するものであり、レンダラーはそれらの自然な解釈をできる限り尊重すべきです。たとえば、mathvariant 属性をもつトークンを Helvetica や Arial のような sans-serif 書体に設定することは合理的ですが、Times Roman フォントでレンダリングすることは非常に誤解を招きやすいので、そのような実装は避けるべきです。
ただし、mathvariant 属性値の自然な解釈は特定の文字に対してのみ有意義である、という問題があります。たとえば、'fraktur'書体のαや、太斜体の漢字は明瞭でわかりやすいレンダリングができません。一般的に、明確に解釈できるのは、SMP Math Alphanumeric Symbol の文字に限定されます。
従って、mathvariant 属性を SMP Math Alphanumeric Symbol 対応する文字に適用する場合は、スタイルシート制作者やプリケーション開発者は、その明確な植字上の解釈をできる限り尊重することが求められますが、それ以外の場合に mathvariant 属性の及ぼす効果については、レンダラーに依存します。
たとえばレンダラーは ∑ (非 SMP 対応文字) を含むトークンについて、mathvariant 属性が bold ないし bold-fraktur に設定される時に太字フォントで表示し、fraktur に設定された時に標準の Roman 書体で表示することができます。
この例からわかるように、制作者は mathvariant 属性を非 SMP 対応文字に対して用いるべきではありません。なぜなら、それは意味がない上に、どのようにレンダリングされるか予想不可能だからです。
最後に、特殊な例として扱われなければならない mathvariant 属性についての冗長性の問題があります。
BMP 文字データ (詳細は 第6.2.3節「Mathematical Alphanumeric Symbols Characters」を参照のこと) の一部の文字を含む mi 要素に mathvariant 属性を用いる場合、レンダリングの結果が SMP 文字を含む mi 要素に mathvariant 属性をもたないものと視覚的に区別できなくなることがあります。
そこで、MathML 2.0 では、これらの2つの表示を等価なものとして扱うよう処理アプリケーションに要求します。
これは、検索や等価性の試験をサポートするアプリケーションための問題を念頭に置いたものです。
第 2.4.5 節「すべての MathML 要素に共通する属性」で述べられているとおり、トークン要素にはスタイルシート機構との互換性のために id, xref, class および style 属性が許容されています。
しかし、CSS を用いる場合には若干の注意が必要です。
式の意味を変えてしまうような視覚的な効果を生むために CSS を用いることは、特に避けるべきです。というのも、MathML は非 CSS 環境で用いられることがあるからです。
同様に、任意の文書全体にわたるスタイルの変換によって、数式に対し意味が変わるなどの影響が及ばないことが保証されるよう注意されるべきです。
しばしば MathML 式は XHTML のようなテキストデータ形式の中に埋め込まれますので、 周囲の文字とMathMLは、レンダリングが互換になるよう、フォントの大きさといったレンダリング属性を共有しなければなりません。 この理由のために、テキストのレンダリングに影響を及ぼすほとんどの属性値は、周囲のレンダリング環境を継承します。これは上記の表の「標準値」の列に示されています。 (周囲のテキストと MathML がブラウザーとプラグインのように 別々のソフトウェアによってレンダリングされる場合も、周囲の文字のベースラインの高さなどといった MathML 属性として定義されていない付加情報とともに MathML レンダラーにレンダリング環境が提供されることが重要です。) ただし、MathML 2.0 はスタイル情報がレンダリング環境から継承されるメカニズムについては定めていないことに注意してください。 たとえば、あるブラウザーのプラグインは CSS 継承メカニズムを完全に利用して CSS プロパティーを完全に解析してレンダリングするかも知れませんし、他のアプリケーションではルートノードのスタイル環境のみを考慮して内部のスタイル継承ルールを利用するかも知れません。
ほとんどの MathML レンダラーは、おそらく付加的な内部スタイル処理アルゴリズムが必要となるでしょう。
特に、mathvariant 属性の継承は CSS モデルとは異なります。
この属性の標準値は mi 以外のすべてのトークンに対して normal (非斜体) であり、mi トークンについて、標準値はトークンの中身の文字数に依存します。
(廃止された fontslant 属性もまたこのような挙動を示しました。)
詳しくは 第3.2.3節「識別子 (mi)」 を参照してください。
下に挙げる MathML 1.01 のスタイル属性は、MathML 2.0 では廃止されました。CSS をサポートするレンダリング環境では、これらの属性に対応する描画プロパティは CSS を用いて制御することが望ましいです。しかし通常は、上で述べたように、これらの描画プロパティをどんな方法であれ直接的に操作することは避けるべきです。
もしも新しい数学用スタイル属性と、それに競合する廃止属性の両方が同時に指定される場合、新しい数学用スタイル属性の値が使われるべきです。たとえば
<mi fontweight='bold' mathvariant='normal'> a </mi>
という指定は、通常の太さのフォントで描画され、
<mi fontweight='bold' mathvariant='sans-serif'> a </mi>
というマークアップは、通常の太さの sans serif 書体で描画されるべきです。
<mi fontweight='bold' mathvariant='fraktur'> a1 </mi>
一般に SMP Math Alphanumeric Symbol 文字ではない '1' には fraktur が適応されませんが、この例では mathvariant 属性によって fontweight 属性がオーバーライドされています。
数字の Fraktur 書体のない環境では、これを Fraktur 書体の 'a' と Roman 書体の '1' で描画するレンダラーが多いでしょう。
廃止された 1.01 のスタイルの属性値は、継承関係についても、新しい数学用スタイル属性によってオーバーライドされます。従って
<mstyle fontstyle='italic'> <mi mathvariant='bold'> a </mi> </mstyle>
というマークアップは、太字の直立な (イタリックではない) フォントで描画されるでしょう。
しかし一方で、MathML 1.01 の属性は依然として役に立ちます。 MathML 1.01 属性は、数学レイアウトに必要な直接描画プロパティに対応するので、 MathML のレイアウト規則とアルゴリズムを記述するのにとても便利だからです。 この理由から、そして後方互換性のために、この章で説明している MathML のレンダリング規則は、引き続き MathML 1.01 のスタイル属性を用いた描画プロパティの用語で記述されています。
廃止された属性は以下の通り:
| 名 | 値 | 標準値 |
|---|---|---|
| fontsize | number v-unit | inherited |
| fontweight | normal | bold | inherited |
| fontstyle | normal | italic | normal (except on <mi>) |
| fontfamily | string | css-fontfamily | inherited |
| color | #rgb | #rrggbb | html-color-name | inherited |
fontsize 属性は、望み通りのフォントサイズを定めます。
v-unit は、垂直長さの単位です
(第2.4.4.3節「CSS互換の属性」を参照してください)。
植字の世界では、フォントサイズを指定するための単位として、一般に pt (ポイント) が用いられます。
もし表示中のフォントでは表示できないフォントサイズが要求された時、レンダラーはもっとも可読性が高く、できうる限り高品質なレンダリングを実現できる方法を選んで、近づけるべきです。
MathML 要素の多くは、子要素について自動的に fontsize を調節します; mstyle の節の scriptlevel の議論を参照してください。→第3.3.4節「スタイルの変更 (mstyle)」
fontfamily 属性の値は、MathML のレンダラーが利用できるフォントの名前であって、レンダラーがそれぞれの方法でフォントを選ぶことができます;
この属性に指定できる値とその意味は、レンダラーやその使用される環境に依存し、MathML によって特定されるものではありません。
(ただし下の css-fontfamily についての注意書きを参照してください)
(レンダラーがフォントを名前で検索するメカニズムは、大文字小文字を区別することがある、ということに注意しましょう)
もし fontfamily の値がレンダラーによって認識できないものであっても、それは MathML のエラーと解釈してはいけません。
むしろレンダラーは、要求されたフォントに最も近い適切なフォントを使用するか、その属性を無視して値の設定をなかったことにするべきです。
fontfamily 属性の使用は、必ずしもすべての MathML のレンダラーで利用可能ではありません。
特に、ASCII 文字ではない MathML 文字への参照を実現する目的で fontname 属性を使ってはいけません (例えば、一般の文字を非ASCIIグリフに対応させているような Symbol フォントの文字への参照を用いる、など (訳注: 記号フォントを使った ゥ → ハート のような表示はやめろ、と。))。
この方針の結果として、MathML レンダラーは、第 6 章「文字、実体とフォント」に挙げられた MathML 文字は、指定されたフォントで利用できない場合でも、適切にレンダリングするよう心がけるべきです。
そうした描画ができないはずはありません
- 最新のレポートによれば、どの文字も、第 6 章「文字、実体とフォント」中の同じ文字に割り当てられた実体名を用いれば XML 風の実体参照 として表現可能、とされているからです。
シンボル css-fontfamily は、CSS の font-family プロパティの legal な値を参照します。
CSS の font-family は、カンマで区切られた代替フォント名ないし一般フォントタイプの優先順位付きリストで、CSS [CSS2] で詳細に記述されています。
MathML レンダラーは、たとえ CSS をサポートしていなくても、レンダリング環境において現実的であればフォント指定に CSS 構文が利用できることが期待されます
(第2.4.4.3節「CSS-互換属性」中のCSS-互換属性についての項目も参照してください)。
mathcolor 属性 (および廃止された color 属性) は、トークンの本体の描画に使われる色を制御します。
さらに、mstyle や MathML 式のレンダリング環境から継承する場合は、他のすべての MathML 要素の描画色を制御します。これには、各種の線や、frac, mtable, msqrt によって指定される記号のたぐいを含みます。
mathcolor, color, mathbackground, background の値は、'#'の後に空白を挟まずに 1 桁ないし 2 桁の 16 進の値で赤、緑、青の色素をそれぞれ指定することで、任意の色を表現することができます ( background に対しては `transparent'というキーワードを用いることができます)。16 進の値は、大文字・小文字を区別しません。
それぞれの色素の値は、1 桁なら 0 (色素が存在しない) から F (色素が100%含まれる) まで、2 桁なら 00 (色素が存在しない) から FF (色素が100%含まれる) まで指定することができます。なお、1 桁の x という値は 2 桁の xx という値 (x0 ではありません) と等価です。% x0 という表記の方がより厳密ですが、ブラウザーによってはレンダリングが崩れることがあります。
これらの属性は、後に説明する html-color-name によって指定することもできます。
上で説明した色の構文は、CSS の color および background-color プロパティの構文のサブセットです。
つまり、background-color 構文もまた CSS の background プロパティの構文の完全なサブセットです。background プロパティを用いれば、たとえば背景画像をタイル状に並べるといった指定もできます。一般的な属性名としての background は、MathML では将来的に属性のスコープの拡張を可能にするために用いられています。
それぞれの属性における色の値は、html-color-name で指定することもできます。これは、[HTML4] で定義されている、色名のキーワード (aqua,
black,
blue,
fuchsia,
gray,
green,
lime,
maroon,
navy,
olive,
purple,
red,
silver,
teal,
white,
yellow) のいずれかです。
色名キーワードは、多くのMathML属性値と異なり、CSSおよびHTMLの互換性のために、大文字小文字を区別しないことに注意してください。
The suggested MathML visual rendering rules do not define the
precise extent of the region whose background is affected by using the
(訳注: この部分は原文の誤植のようで、のちに出てくるPrecise background region not specifiedが混入してしまったようです)
background attribute on mstyle,
except that, when mstyle's content does not have
negative dimensions and its drawing region is not overlapped by other
drawing due to surrounding negative spacing, this region should lie
behind all the drawing done to render the content of the
mstyle, but should not lie behind any of the
drawing done to render surrounding expressions. The effect of overlap
of drawing regions caused by negative spacing on the extent of the
region affected by the background attribute is not
defined by these rules.
mi)mi 要素は、識別子(identifier)として描画されるシンボル名や任意のテキストを表現するためのものです。識別子には、変数、関数名、およびシンボル定数を含みます。
必ずしもすべての「数学識別子」(mathematical identifiers) が mi によって表現されるわけではありません - たとえば、下付文字やプライムを伴う変数は、それぞれ msub や msup によって表現されます。
逆に、級数の合計における省略記号のような、「ターム」としての意味を持つ任意のテキストは、mi で表現することができます。この例は 第3.2.6.4節「Mixing text and mathematics」 に挙げられています。
ここで強調しておきたいのは、miは、プレゼンテーション要素であり、従って、その本体が識別子としてレンダリングされるという意味のみをもつ、ということです。
多くの場合、mi 要素の本体は、実際に変数や関数名といった数学識別子を表現します。
しかし、次の段落で説明されるように、識別子であるかのようにレンダリングされる表記と、実際に数学識別子を表現するべき表記の対応は完全ではありません。
その意味が識別子として保証されている要素については、第4章「コンテンツ・マークアップ」 中の ci の説明を参照してください。
mi 要素は、第3.2.2節「トークン要素に共通な数学用スタイル属性」 で挙げられる属性をもつことができますが、
デフォルトの属性値が異なるものがあります:
| 名前 | 値 | デフォルト |
|---|---|---|
| mathvariant | normal | bold | italic | bold-italic | double-struck | bold-fraktur | script | bold-script | fraktur | sans-serif | bold-sans-serif | sans-serif-italic | sans-serif-bold-italic | monospace | (本体に依存; 下で説明します) |
| fontstyle (廃止属性) | normal | italic | (本体に依存; 下で説明します) |
典型的なグラフィカルレンダラーは、mi 要素を描画する際、その周囲に余分な空白をもたないように(周辺要素との間の空白を除く)、要素の本体として含まれる文字を描画するでしょう。
mathvariant および fontstyle のデフォルト値は、要素の本体が一文字でなければ、通常 normal (non-slanted) になりますが、一文字の場合には italic になります。
この規則は mi 要素のみの mathvariant および fontstyle 属性のものである、ということに注意してください;
その他の要素に対する mathvariant および fontstyle 属性のデフォルト値は、(常に) normal です。
数学用英数字記号の文字 (第6.2.3節「数学用英数字記号の文字」 および 第3.2.1.1節「英数字記号の文字」 をご覧下さい) の対応文字を決定する目的のために、上で述べた特殊なデフォルト値に対する挙動を含め、mathvariant 属性の値が最初に解決されることに注意してください。
<mi> x </mi> <mi> D </mi> <mi> sin </mi> <mi mathvariant='script'> L </mi> <mi></mi>
本体を含まない mi 要素もありえます;
たとえば、<mi></mi> という表記は、
(従来の数学構文に従えば) 必要とされる「ターム」をまだ含んでいない MathML 式において、タームの位置を表すために「式エディター」が用いることがあります。
識別子には、「sin」のような関数名が含まれます。
「sin x」のような式は、次のように ⁡ 演算子 (省略名 ⁡ もあります) を用いて書かれるべきです;
第3.2.5節「演算子、囲い文字、区切り文字、アクセント (mo)」 の不可視の演算子についての議論も参照してください。
<mrow> <mi> sin </mi> <mo> ⁡ </mo> <mi> x </mi> </mrow>
「ターム」として扱われるべきその他のテキストは、mi 要素を用いて表現することができます。たとえば:
<mrow> <mn> 1 </mn> <mo> + </mo> <mi> ... </mi> <mo> + </mo> <mi> n </mi> </mrow>
このような例外的な状況で mi が用いられる場合には、
明示的に fontstyle 属性を指定することにより、一部のブラウザーでデフォルトの挙動よりもよい結果が得られることがあります。
シンボル定数名は、mi 要素によって表現されます:
<mi> π </mi> <mi> ⅈ </mi> <mi> ⅇ </mi>
このような定数を表す特別な実体参照を用いることで、MathML のプレゼンテーション要素の解釈が簡単になります。 See Chapter 6 [Characters, Entities and Fonts] for a complete list of character entity references in MathML.
mn)mn 要素は、「数リテラル」や、数リテラルとしてとして描画されるべきその他のデータを表します。一般的に数リテラルは、符号なし整数や実数を表現し、小数点を含みうる数字の連続のことです。
数学における「数」の概念は、非常に微妙で複雑であり、文脈によって異なります。
従って、必ずしも数学上のすべての数が mn を用いて表現されるべきというわけではありません;
数学上の数の異なる表現方法の例を以下に示します。複素数、分数で表される割合、数定数の名前、などを含みます。
数を文字列としてエンコーディングする標準的な方法を用いると、mn 本体の数としての解釈が曖昧になってしまうことがあります。
そのような場合においても、mn はプレゼンテーション要素なので、数リテラルとして描画されることのないその他一般のテキストを mn の本体の中に含むことが望ましい場合がごくまれにあり得ます。
しかし原則的には、mn 要素は、
その本体が実際になんらかの方法で数量を表す場合に用いられるべきです。
何らかの形で数学的な数としての意味が保証されている要素については、
第4章「コンテンツ・マークアップ」 中の cn についての説明を参照してください。
mn 要素は、第3.2.2節「トークン要素に共通な数学用のスタイル属性」 で挙げられた属性を受け付けます。
典型的なグラフィカル・レンダラーは、mn 要素の本体の文字を、その周囲に特別な空白をつけず、そのまま描画するでしょう (ただし、mo のような要素と隣接する場合には空白をおきます)。
mi とは異なり、mn 要素は、(通常) その本体に拘わらず標準で直立な (unslanted) フォントで描画されます。
<mn> 2 </mn> <mn> 0.123 </mn> <mn> 1,000,000 </mn> <mn> 2.1e10 </mn> <mn> 0xFFEF </mn> <mn> MCMLXIX </mn> <mn> twenty one </mn>
mn のみを用いて記述されるべきではない数多くの数学上の数は、mn だけではなく、他のプレゼンテーション要素を用いて表されるべきです; これには、複素数や、分数で表される割合、数定数の名前などが含まれます。このような MathML 表現の例は、以下のようになります:
<mrow>
<mn> 2 </mn>
<mo> + </mo>
<mrow>
<mn> 3 </mn>
<mo> ⁢ </mo>
<mi> ⅈ </mi>
</mrow>
</mrow>
<mfrac> <mn> 1 </mn> <mn> 2 </mn> </mfrac>
<mi> π </mi>
<mi> ⅇ </mi>
mo)mo要素は、演算子もしくは演算子として描画されるべきその他のものを表します。
一般的に、数学で用いられる演算子の表記に関する慣習はとても複雑で、ゆえに MathML では mo 要素のレンダリングの挙動について、やや洗練されたメカニズムを採用しています。
その結果、MathML では従来は数学的な演算子として扱われなかった多くの表記を「演算子として描画される」べきものに含めるようになりました。
これらには、挿入辞・接頭辞・接尾辞の形式をを含めた従来の演算子以外に、大括弧・丸括弧・絶対値記号のような囲い文字、カンマやセミコロンのような区切り文字、そして記号の上部に付けるバーやチルダなどのような数学的なアクセントが含まれます。
用語「演算子」は、この章では演算子として描画されるべき記号ないし表記のことを意味します。従って演算子は、mo によって表されます。つまり、特に指定がなく文脈からも明らかではない場合には、用語「演算子」に既存の演算子、囲い文字、区切り文字、アクセントを含むということです。
このような記号は、基本的に同じレンダリング属性・レンダリング規則に属しているため、MathML ではすべて mo 要素で表されます; レンダリングにおいて記号の種類による些細な区別があれば、ブール (boolean) 属性である fence、separator、accent を用いてその区別を行います。
mo 要素のもっとも大切な特徴は、そのデフォルト値が次に説明するように「演算子辞書」から場合に応じて決定されるということです。特に、fence、separator、accent のデフォルト値は一般に演算子辞書から選ばれ、従って、それぞれの mo 要素に対して個別に指定する必要がありません。
数学演算子の中には、mo 要素のみではなく、(たとえば)周囲の上付き文字によって修飾された mo 要素によって表されるものもあることに注意してください (このことについては後にさらに記述しています)。一方、mo 要素はプレゼンテーション要素なので、
テキストが一般には演算子として扱われない場合でも一般的なテキストを mo 要素に含むことができます。
たとえば、第3.2.6節「テキスト (mtext)」中の「テキストと数学の混合」の議論をご覧下さい。MathML で特定の数学演算子としての意味を含むことが保証されたコンテンツ要素の定義については第4章「コンテンツ・マークアップ」も参照してください。
mo 要素は、
第3.2.2節「トークン要素に共通な数学スタイル属性」 で挙げられた属性と、ここで挙げる追加的な属性ををとることができます。
多くの属性のデフォルト値は、この節の後で述べるとおり 第3.2.5.7.1節「演算子辞書」 にあります。
与えられた mo 要素が辞書のエントリーとして見つからない場合は、ここで括弧付きで示されるデフォルト値が用いられます。
mo elements accept the attributes listed in
Section 3.2.2 [Mathematics style attributes common to token
elements], and the additional attributes listed here.
Most attributes get their default values from the
Section 3.2.5.7.1 [The operator dictionary], as described later in this
section. When a dictionary entry is not found for a given
mo element, the default value shown here in
parentheses is used.
| 属性名 Name |
値 values |
デフォルト default |
|---|---|---|
| form | prefix | infix | postfix |
mrow の中での演算子の位置による (規則は後述);
mo の本体とともに演算子辞書をインデックス付けするために用いられる
set by position of operator in an mrow (rule given below);
used with mo content to index operator dictionary |
| fence | true | false | 辞書によって決定 (false) set by dictionary (false) |
| separator | true | false | 辞書によって決定 (false) set by dictionary (false) |
| lspace | number h-unit | namedspace | 辞書によって決定 (thickmathspace) set by dictionary (thickmathspace) |
| rspace | number h-unit | namedspace | 辞書によって決定 (thickmathspace) set by dictionary (thickmathspace) |
| stretchy | true | false | 辞書によって決定 (false) set by dictionary (false) |
| symmetric | true | false | 辞書によって決定 (true) set by dictionary (true) |
| maxsize | number [ v-unit | h-unit ] | namedspace | infinity | 辞書によって決定 (infinity) set by dictionary (infinity) |
| minsize | number [ v-unit | h-unit ] | namedspace | 辞書によって決定 (1) set by dictionary (1) |
| largeop | true | false | 辞書によって決定 (false) set by dictionary (false) |
| movablelimits | true | false | 辞書によって決定 (false) set by dictionary (false) |
| accent | true | false | 辞書によって決定 (false) set by dictionary (false) |
h-unit represents a unit of horizontal
length, and v-unit represents a unit of vertical
length (see
Section 2.4.4.2 [Attributes with units]).
namedspace is one of
veryverythinmathspace,
verythinmathspace,
thinmathspace,
mediummathspace,
thickmathspace,
verythickmathspace, or
veryverythickmathspace.
These values can be set by using the mstyle element
as is further discussed in Section 3.3.4 [Style Change (mstyle)].
If no unit is given with maxsize or minsize, the number is a multiplier of the normal size
of the operator in the direction (or directions) in which it stretches.
These attributes are further explained below.
Typical graphical renderers show all mo
elements as the characters of their content, with additional spacing
around the element determined from the attributes listed
above. Detailed rules for determining operator spacing in visual
renderings are described in a subsection below. As always, MathML does
not require a specific rendering, and these rules are provided as
suggestions for the convenience of implementors.
Renderers without access to complete fonts for the MathML character
set may choose not to render an mo element as
precisely the characters in its content in some cases. For example,
<mo> ≤ </mo> might be rendered as
<= to a terminal. However, as a general rule,
renderers should attempt to render the content of an
mo element as literally as possible.
That is,
<mo> ≤ </mo> and
<mo> <= </mo> should render differently.
(The first one should render as a single character
representing a less-than-or-equal-to sign, and the second one as the
two-character sequence <=.)
<mo> + </mo> <mo> < </mo> <mo> ≤ </mo> <mo> <= </mo> <mo> ++ </mo> <mo> ∑ </mo> <mo> .NOT. </mo> <mo> and </mo> <mo> ⁢ </mo> <mo mathvariant='bold'> + </mo>
Note that the mo elements in these examples
don't need explicit fence or separator attributes, since these can be found using the
operator dictionary as described below. Some of these examples could also
be encoded using the mfenced element described in
Section 3.3.8 [Expression Inside Pair of Fences
(mfenced)].
(a+b)
<mrow>
<mo> ( </mo>
<mrow>
<mi> a </mi>
<mo> + </mo>
<mi> b </mi>
</mrow>
<mo> ) </mo>
</mrow>
[0,1)
<mrow>
<mo> [ </mo>
<mrow>
<mn> 0 </mn>
<mo> , </mo>
<mn> 1 </mn>
</mrow>
<mo> ) </mo>
</mrow>
f(x,y)
<mrow>
<mi> f </mi>
<mo> ⁡ </mo>
<mrow>
<mo> ( </mo>
<mrow>
<mi> x </mi>
<mo> , </mo>
<mi> y </mi>
</mrow>
<mo> ) </mo>
</mrow>
</mrow>
Certain operators that are `invisible' in traditional
mathematical notation should be represented using specific entity
references within mo elements, rather than simply
by nothing. The entity references used for these `invisible
operators' are:
| Full name | Short name | Examples of use |
|---|---|---|
⁢ |
⁢ |
xy |
⁡ |
⁡ |
f(x) sin x |
⁣ |
⁣ |
m12 |
The MathML representations of the examples in the above table are:
<mrow>
<mi> x </mi>
<mo> ⁢ </mo>
<mi> y </mi>
</mrow>
<mrow>
<mi> f </mi>
<mo> ⁡ </mo>
<mrow>
<mo> ( </mo>
<mi> x </mi>
<mo> ) </mo>
</mrow>
</mrow>
<mrow>
<mi> sin </mi>
<mo> ⁡ </mo>
<mi> x </mi>
</mrow>
<msub>
<mi> m </mi>
<mrow>
<mn> 1 </mn>
<mo> ⁣ </mo>
<mn> 2 </mn>
</mrow>
</msub>
The reasons for using specific mo elements for
invisible operators include:
mspace or mtext
elements;
For example, an audio renderer might render f(x)
(represented as in the above examples) by speaking `f of x', but use
the word `times' in its rendering of xy.
Although its rendering must still be different depending on the structure
of neighboring elements (sometimes leaving out `of' or
`times' entirely), its task is made much easier by the use of
a different mo element for each invisible
operator.
MathML also includes ⅆ for use
in an mo element representing the differential
operator symbol usually denoted by `d'. The reasons for
explicitly using this special entity are similar to those for using
the special entities for invisible operators described in the
preceding section.
mo elementsTypical visual rendering behaviors for mo
elements are more complex than for the other MathML token elements, so
the rules for rendering them are described in this separate
subsection.
Note that, like all rendering rules in MathML, these rules are suggestions rather than requirements. Furthermore, no attempt is made to specify the rendering completely; rather, enough information is given to make the intended effect of the various rendering attributes as clear as possible.
Many mathematical symbols, such as an integral sign, a plus sign,
or a parenthesis, have a well-established, predictable, traditional
notational usage. Typically, this usage amounts to certain default
attribute values for mo elements with specific
contents and a specific form attribute. Since these
defaults vary from symbol to symbol, MathML anticipates that renderers
will have an `operator dictionary' of default attributes for
mo elements (see Appendix F [Operator Dictionary]) indexed by each
mo element's content and form
attribute. If an mo element is not listed in the
dictionary, the default values shown in parentheses in the table of
attributes for mo should be used, since these
values are typically acceptable for a generic operator.
Some operators are `overloaded', in the sense that they can occur
in more than one form (prefix, infix, or postfix), with possibly
different rendering properties for each form. For example, `+' can be
either a prefix or an infix operator. Typically, a visual renderer
would add space around both sides of an infix operator, while only on
the left of a prefix operator. The form attribute allows
specification of which form to use, in case more than one form is
possible according to the operator dictionary and the default value
described below is not suitable.
form attributeThe form attribute does not usually have to be
specified explicitly, since there are effective heuristic rules for
inferring the value of the form attribute from the
context. If it is not specified, and there is more than one possible
form in the dictionary for an mo element with
given content, the renderer should choose which form to use as follows
(but see the exception for embellished operators, described later):
mrow of length (i.e. number of arguments) greater than
one (ignoring all space-like arguments (see Section 3.2.7 [Space (mspace)]) in the
determination of both the length and the first argument), the prefix form
is used;
mrow of
length greater than one (ignoring all space-like arguments), the postfix
form is used;
mrow, the infix form is used.
Note that these rules make reference to the
mrow in which the mo
element lies. In some situations, this mrow
might be an inferred mrow implicitly present
around the arguments of an element such as
msqrt or mtd.
Opening (left) fences should have form="prefix",
and closing (right) fences should have form="postfix";
separators are usually `infix', but not always,
depending on their surroundings. As with ordinary operators,
these values do not usually need to be specified explicitly.
If the operator does not occur in the dictionary with the specified
form, the renderer should use one of the forms that is available
there, in the order of preference: infix, postfix, prefix; if no forms
are available for the given mo element content, the
renderer should use the defaults given in parentheses in the table of
attributes for mo.
There is one exception to the above rules for choosing an mo element's default form
attribute. An mo element that is
`embellished' by one or more nested subscripts, superscripts,
surrounding text or whitespace, or style changes behaves differently. It is
the embellished operator as a whole (this is defined precisely, below)
whose position in an mrow is examined by the above
rules and whose surrounding spacing is affected by its form, not the mo element at its core; however, the attributes
influencing this surrounding spacing are taken from the mo element at the core (or from that element's
dictionary entry).
For example, the `+4' in
a+4b
should be considered an infix operator as a whole, due to its position
in the middle of an mrow, but its rendering
attributes should be taken from the mo element
representing the `+', or when those are not specified explicitly,
from the operator dictionary entry for <mo form="infix"> +
</mo>.
The precise definition of an `embellished operator' is:
mo element;
msub,
msup,
msubsup,
munder,
mover,
munderover,
mmultiscripts,
mfrac, or
semantics
(Section 4.2.6 [Syntax and Semantics]), whose first argument exists and is an embellished
operator;
mstyle,
mphantom, or
mpadded,
such that an mrow containing the same
arguments would be an embellished operator;
maction element whose selected
sub-expression exists and is an embellished operator; mrow whose arguments consist (in any order)
of one embellished operator and zero or more space-like elements.
Note that this definition permits nested embellishment only when there are no intervening enclosing elements not in the above list.
The above rules for choosing operator forms and defining
embellished operators are chosen so that in all ordinary cases it will
not be necessary for the author to specify a form
attribute.
The following notes are included as a rationale for certain aspects of the above definitions, but should not be important for most users of MathML.
An mfrac is included as an
`embellisher' because of the common notation for a
differential operator:
<mfrac>
<mo> ⅆ </mo>
<mrow>
<mo> ⅆ </mo>
<mi> x </mi>
</mrow>
</mfrac>
Since the definition of embellished operator affects the use of the
attributes related to stretching, it is important that it includes
embellished fences as well as ordinary operators; thus it applies to
any mo element.
Note that an mrow containing a single argument
is an embellished operator if and only if its argument is an embellished
operator. This is because an mrow with a single
argument must be equivalent in all respects to that argument alone (as
discussed in Section 3.3.1 [Horizontally Group Sub-Expressions
(mrow)]). This means that an mo element that is the sole argument of an mrow will determine its default form attribute based on that mrow's position in a surrounding, perhaps inferred, mrow (if there is one), rather than based on its own
position in the mrow in which it is the sole
argument.
Note that the above definition defines every
mo element to be `embellished' - that is,
`embellished operator' can be considered (and implemented in
renderers) as a special class of MathML expressions, of which
mo is a specific case.
The amount of space added around an operator (or embellished operator),
when it occurs in an mrow, can be directly
specified by the lspace and rspace attributes. These values are in ems if no units
are given. By convention, operators that tend to bind tightly to their
arguments have smaller values for spacing than operators that tend to bind
less tightly. This convention should be followed in the operator dictionary
included with a MathML renderer. In TEX, these values can only be one of
three values; typically they are 3/18em, 4/18em, and 5/18em. MathML does
not impose this limit.
Some renderers may choose to use no space around most operators appearing within subscripts or superscripts, as is done in TEX.
Non-graphical renderers should treat spacing attributes, and other rendering attributes described here, in analogous ways for their rendering medium. For example, more space might translate into a longer pause in an audio rendering.
Four attributes govern whether and how an operator (perhaps embellished)
stretches so that it matches the size of other elements: stretchy, symmetric, maxsize, and minsize. If an
operator has the attribute stretchy=true, then it (that is, each character in its content)
obeys the stretching rules listed below, given the constraints imposed by
the fonts and font rendering system. In practice, typical renderers will
only be able to stretch a small set of characters, and quite possibly will
only be able to generate a discrete set of character sizes.
There is no provision in MathML for specifying in which direction
(horizontal or vertical) to stretch a specific character or operator;
rather, when stretchy=true it
should be stretched in each direction for which stretching is possible. It
is up to the renderer to know in which directions it is able to stretch
each character. (Most characters can be stretched in at most one direction
by typical renderers, but some renderers may be able to stretch certain
characters, such as diagonal arrows, in both directions independently.)
The minsize and maxsize
attributes limit the amount of stretching (in either direction). These two
attributes are given as multipliers of the operator's normal size in the
direction or directions of stretching, or as absolute sizes using units.
For example, if a character has maxsize="3", then it
can grow to be no more than three times its normal (unstretched) size.
The symmetric attribute governs whether the
height and
depth above and below the axis of the
character are forced to be equal
(by forcing both height and depth to become the maximum of the two).
An example of a situation where one might set
symmetric=false
arises with parentheses around a matrix not aligned on the axis, which
frequently occurs when multiplying non-square matrices. In this case, one
wants the parentheses to stretch to cover the matrix, whereas stretching
the parentheses symmetrically would cause them to protrude beyond one edge
of the matrix. The symmetric attribute only applies
to characters that stretch vertically (otherwise it is ignored).
If a stretchy mo element is embellished (as defined
earlier in this section), the mo element at its core is
stretched to a size based on the context of the embellished operator
as a whole, i.e. to the same size as if the embellishments were not
present. For example, the parentheses in the following example (which
would typically be set to be stretchy by the operator dictionary) will be
stretched to the same size as each other, and the same size they would
have if they were not underlined and overlined, and furthermore will
cover the same vertical interval:
<mrow>
<munder>
<mo> ( </mo>
<mo> _ </mo>
</munder>
<mfrac>
<mi> a </mi>
<mi> b </mi>
</mfrac>
<mover>
<mo> ) </mo>
<mo> ‾ </mo>
</mover>
</mrow>
Note that this means that the stretching rules given below must
refer to the context of the embellished operator as a whole, not just
to the mo element itself.
This shows one way to set the maximum size of a parenthesis so that
it does not grow, even though its default value is
stretchy=true.
<mrow>
<mo maxsize="1"> ( </mo>
<mfrac>
<mi> a </mi> <mi> b </mi>
</mfrac>
<mo maxsize="1"> ) </mo>
</mrow>
The above should render as
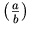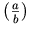 as opposed to the default rendering
as opposed to the default rendering
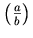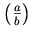 .
.
Note that each parenthesis is sized independently; if only one of
them had maxsize="1", they would render with different
sizes.
mrow element, or is the sole direct sub-expression of an
mtd element in some row of a table, then it should
stretch to cover the height and depth (above and below the axis) of the non-stretchy direct sub-expressions in the
mrow element or table row, unless stretching is
constrained by minsize or maxsize attributes.
symmetric=true,
then the maximum of the height and depth is used to determine the size,
before application of the minsize or maxsize attributes.
mrow element is inferred.
Most common opening and closing fences are defined in the operator
dictionary to stretch by default; and they stretch vertically. Also,
operators such as ∑, ∫,
/, and vertical arrows stretch vertically by default.
In the case of a stretchy operator in a table cell (i.e. within an
mtd element), the above rules assume each cell of
the table row containing the stretchy operator covers exactly one row.
(Equivalently, the value of the rowspan attribute is
assumed to be 1 for all the table cells in the table row, including
the cell containing the operator.) When this is not the case, the
operator should only be stretched vertically to cover those table
cells that are entirely within the set of table rows that the
operator's cell covers. Table cells that extend into rows not covered
by the stretchy operator's table cell should be ignored. See
Section 3.5.4.2 [Attributes] for details about the rowspan attribute.
munder,
mover, or munderover element,
or if it is the sole direct sub-expression of an mtd element in some
column of a table (see mtable), then it, or the mo element at its core, should stretch to cover
the width of the other direct sub-expressions in the given element (or
in the same table column), given the constraints mentioned above.
munder, mover, or
munderover element, or if it is the sole direct
sub-expression of an mtd element in some column of a
table, then it should stretch to cover the width of the other direct
sub-expressions in the given element (or in the same table column),
given the constraints mentioned above.
By default, most horizontal arrows and some accents stretch horizontally.
In the case of a stretchy operator in a table cell (i.e. within an
mtd element), the above rules assume each cell of
the table column containing the stretchy operator covers exactly one
column. (Equivalently, the value of the columnspan
attribute is assumed to be 1 for all the table cells in the table row,
including the cell containing the operator.) When this is not the
case, the operator should only be stretched horizontally to cover
those table cells that are entirely within the set of table columns
that the operator's cell covers. Table cells that extend into columns
not covered by the stretchy operator's table cell should be
ignored. See Section 3.5.4.2 [Attributes] for details about the rowspan attribute.
The rules for horizontal stretching include mtd
elements to allow arrows to stretch for use in commutative diagrams
laid out using mtable. The rules for the horizontal
stretchiness include scripts to make examples such as the following
work:
<mrow>
<mi> x </mi>
<munder>
<mo> → </mo>
<mtext> maps to </mtext>
</munder>
<mi> y </mi>
</mrow>
This displays as
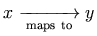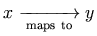 .
.
If a stretchy operator is not required to stretch (i.e. if it is not in one of the locations mentioned above, or if there are no other expressions whose size it should stretch to match), then it has the standard (unstretched) size determined by the font and current fontsize.
If a stretchy operator is required to stretch, but all other expressions
in the containing element (as described above) are also stretchy,
all elements that can stretch should grow to the maximum of the normal
unstretched sizes of all elements in the containing object, if they can
grow that large. If the value of minsize or maxsize prevents this then that (min or max) size is
used.
For example, in an mrow containing nothing but
vertically stretchy operators, each of the operators should stretch to
the maximum of all of their normal unstretched sizes, provided no
other attributes are set that override this behavior. Of course,
limitations in fonts or font rendering may result in the final,
stretched sizes being only approximately the same.
mo
The largeop attribute specifies whether the
operator should be drawn larger than normal if displaystyle=true in the current
rendering environment. This roughly corresponds to TEX's
\displaystyle style setting. MathML uses two attributes, displaystyle and scriptlevel, to
control orthogonal presentation features that TEX encodes into one
`style' attribute with values \displaystyle,
\textstyle, \scriptstyle, and
\scriptscriptstyle. These attributes are discussed further in
Section 3.3.4 [Style Change (mstyle)] describing the mstyle element.
Note that these attributes can be specified directly on an mstyle element's start tag, but not on most other
elements. Examples of large operators include ∫
and ∏.
The movablelimits attribute specifies whether
underscripts and overscripts attached to this mo
element should be drawn as subscripts and superscripts when displaystyle=false. movablelimits=false means that
underscripts and overscripts should never be drawn as subscripts and
superscripts. In general, displaystyle is true for displayed mathematics and false for inline mathematics. Also, displaystyle is false by default
within tables, scripts and fractions, and a few other exceptional
situations detailed in Section 3.3.4 [Style Change (mstyle)]. Thus, operators with
movablelimits=true will
display with limits (i.e. underscripts and overscripts) in displayed
mathematics, and with subscripts and superscripts in inline mathematics,
tables, scripts and so on. Examples of operators that typically have movablelimits=true are sum, prod, and lim.
The accent attribute determines whether this
operator should be treated by default as an accent (diacritical mark) when
used as an underscript or overscript; see munder,
mover, and munderover
(Section 3.4.4 [Underscript (munder)], Section 3.4.5 [Overscript (mover)] and Section 3.4.6 [Underscript-overscript Pair
(munderover)]).
The separator attribute may affect automatic
linebreaking in renderers that position ordinary infix operators at
the beginnings of broken lines rather than at the ends (that is, which
avoid linebreaking just after such operators), since linebreaking
should be avoided just before separators, but is acceptable just after
them.
The fence attribute has no effect in the suggested
visual rendering rules given here; it is not needed for properly
rendering traditional notation using these rules. It is provided so
that specific MathML renderers, especially non-visual renderers, have
the option of using this information.
mtext)An mtext element is used to represent
arbitrary text that should be rendered as itself. In general, the
mtext element is intended to denote commentary
text.
Note that some text with a clearly defined notational role might be
more appropriately marked up using mi or
mo; this is discussed further below.
An mtext element can be used to contain
`renderable whitespace', i.e. invisible characters that are
intended to alter the positioning of surrounding elements. In non-graphical
media, such characters are intended to have an analogous effect, such as
introducing positive or negative time delays or affecting rhythm in an
audio renderer. This is not related to any whitespace in the source MathML
consisting of blanks, newlines, tabs, or carriage returns; whitespace
present directly in the source is trimmed and collapsed, as described in
Section 2.4.6 [Collapsing Whitespace in Input]. Whitespace that is intended to be rendered
as part of an element's content must be represented by entity references
or mspace elements
(unless it consists only of single blanks between non-whitespace
characters).
Renderable whitespace can have a positive or negative width, as in   and ​,
or zero width, as in ​. The complete
list of such characters is given in Chapter 6 [Characters, Entities and Fonts]. Note that there
is no formal distinction in MathML between renderable whitespace characters
and any other class of characters, in mtext or in
any other element.
Renderable whitespace can also include characters that affect alignment or linebreaking. Some of these characters are:
| Entity name | Purpose (rough description) |
|---|---|
| 
 | start a new line and do not indent |
| &IndentingNewLine; | start a new line and do indent |
| ⁠ | do not allow a linebreak here |
| &GoodBreak; | if a linebreak is needed on the line, here is a good spot |
| &BadBreak; | if a linebreak is needed on the line, try to avoid breaking here |
For the complete list of MathML entities, consult Chapter 6 [Characters, Entities and Fonts].
mtext elements accept the attributes listed in
Section 3.2.2 [Mathematics style attributes common to token
elements].
See also the warnings about the legal grouping of `space-like
elements' in Section 3.2.7 [Space (mspace)], and about the use of
such elements for `tweaking' or conveying meaning in Section 3.3.6 [Adjust Space Around Content
(mpadded)].
<mtext> Theorem 1: </mtext> <mtext>   </mtext> <mtext>      </mtext> <mtext> /* a comment */ </mtext>
In some cases, text embedded in mathematics could be more appropriately
represented using mo or mi elements.
For example, the expression `there exists
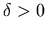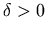 such that f(x) <1' is equivalent to
such that f(x) <1' is equivalent to
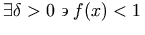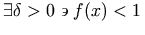 and could be represented as:
and could be represented as:
<mrow>
<mo> there exists </mo>
<mrow>
<mrow>
<mi> δ </mi>
<mo> > </mo>
<mn> 0 </mn>
</mrow>
<mo> such that </mo>
<mrow>
<mrow>
<mi> f </mi>
<mo> ⁡ </mo>
<mrow>
<mo> ( </mo>
<mi> x </mi>
<mo> ) </mo>
</mrow>
</mrow>
<mo> < </mo>
<mn> 1 </mn>
</mrow>
</mrow>
</mrow>
An example involving an mi element is:
x+x2+···+xn.
In this example, ellipsis should be represented using an mi element, since it takes the place of a term in the
sum; (see Section 3.2.3 [Identifier (mi)]).
On the other hand, expository text within MathML is best
represented with an mtext element. An example
of this is:
Theorem 1: if x > 1, then x2 > x.
However, when MathML is embedded in HTML, or another document markup language, the example is probably best rendered with only the two inequalities represented as MathML at all, letting the text be part of the surrounding HTML.
Another factor to consider in deciding how to mark up text is the
effect on rendering. Text enclosed in an mo
element is unlikely to be found in a renderer's operator dictionary,
so it will be rendered with the format and spacing appropriate for an
`unrecognized operator', which may or may not be better than the
format and spacing for `text' obtained by using an
mtext element. An ellipsis entity in an
mi element is apt to be spaced more appropriately
for taking the place of a term within a series than if it appeared in
an mtext element.
mspace)An mspace empty element represents a blank
space of any desired size, as set by its attributes. It can also be
used to make linebreaking suggestions to a visual renderer.
Note that the default values for attributes have been chosen so that
they typically will have no effect on rendering. Thus, the mspace element is generally used with one
or more attribute values explicitly specified.
In addition to the attributes listed below,
mspace permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| width | number h-unit | namedspace | 0em |
| height | number v-unit | 0ex |
| depth | number v-unit | 0ex |
| linebreak | auto | newline | indentingnewline | nobreak | goodbreak | badbreak | auto |
h-unit and v-unit
represent units of horizontal or vertical length, respectively (see
Section 2.4.4.2 [Attributes with units]).
The linebreak attribute is used to give a
linebreaking hint to a visual renderer. The default value is auto, which indicates that a renderer should use
whatever default linebreaking algorithm it would normally use. The
meaning of the other possible values for the linebreak attribute are described above in the
discussion on renderable whitespace in the mtext element. See Section 3.2.6 [Text (mtext)]
for details.
In the case when both dimensional attributes and a linebreaking attribute are set, the linebreaking attribute is ignored.
Note the warning about the legal grouping of `space-like elements'
given below, and the warning about the use of such elements for
`tweaking' or conveying meaning in Section 3.3.6 [Adjust Space Around Content
(mpadded)]. See also the other
elements that can render as whitespace, namely
mtext, mphantom, and
maligngroup.
A number of MathML presentation elements are `space-like' in the
sense that they typically render as whitespace, and do not affect the
mathematical meaning of the expressions in which they appear. As a
consequence, these elements often function in somewhat exceptional
ways in other MathML expressions. For example, space-like elements are
handled specially in the suggested rendering rules for
mo given in Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)].
The following MathML elements are defined to be `space-like':
mtext, mspace,
maligngroup, or malignmark
element; mstyle, mphantom, or
mpadded element, all of whose direct sub-expressions
are space-like; maction element whose selected
sub-expression exists and is space-like; mrow all of whose direct
sub-expressions are space-like.
Note that an mphantom is not
automatically defined to be space-like, unless its content is
space-like. This is because operator spacing is affected by whether
adjacent elements are space-like. Since the
mphantom element is primarily intended as an aid
in aligning expressions, operators adjacent to an
mphantom should behave as if they were adjacent
to the contents of the mphantom,
rather than to an equivalently sized area of whitespace.
Authors who insert space-like elements or
mphantom elements into an existing MathML
expression should note that such elements are counted as
arguments, in elements that require a specific number of arguments,
or that interpret different argument positions differently.
Therefore, space-like elements inserted into such a MathML element
should be grouped with a neighboring argument of that element by
introducing an mrow for that purpose. For example,
to allow for vertical alignment on the right edge of the base of a
superscript, the expression
<msup> <mi> x </mi> <malignmark edge="right"/> <mn> 2 </mn> </msup>
is illegal, because msup must have exactly 2 arguments;
the correct expression would be:
<msup>
<mrow>
<mi> x </mi>
<malignmark edge="right"/>
</mrow>
<mn> 2 </mn>
</msup>
See also the warning about `tweaking' in
Section 3.3.6 [Adjust Space Around Content
(mpadded)].
ms)The ms element is used to represent
`string literals' in expressions meant to be interpreted by
computer algebra systems or other systems containing `programming
languages'. By default, string literals are displayed surrounded by
double quotes. As explained in Section 3.2.6 [Text (mtext)], ordinary text
embedded in a mathematical expression should be marked up with mtext, or in some cases mo or
mi, but never with ms.
Note that the string literals encoded by ms
are `Unicode strings' rather than `ASCII
strings'. In practice, non-ASCII characters will typically be
represented by entity references. For example,
<ms>&</ms> represents a
string literal containing a single character, &, and
<ms>&amp;</ms> represents a
string literal containing 5 characters, the first one of which is
&.
Like all token elements, ms does trim and
collapse whitespace in its content according to the rules of
Section 2.4.6 [Collapsing Whitespace in Input], so whitespace intended to remain in
the content should be encoded as described in that section.
ms elements accept the attributes listed in
Section 3.2.2 [Mathematics style attributes common to token
elements], and additionally:
| Name | values | default |
|---|---|---|
| lquote | string | " |
| rquote | string | " |
In visual renderers, the content of an ms
element is typically rendered with no extra spacing added around the
string, and a quote character at the beginning and the end of the
string. By default, the left and right quote characters are both the
standard double quote character ". However,
these characters can be changed with the lquote and
rquote attributes respectively.
The content of ms elements should be rendered
with visible `escaping' of certain characters in the content,
including at least `double quote' itself, and preferably whitespace
other than individual space characters. The intent is for the viewer to see that
the expression is a string literal, and to see exactly which
characters form its content. For example, <ms>double quote is
"</ms> might be rendered as "double quote is
\"".
mglyph)Unicode defines a large number of characters used in mathematics, and in most cases, glyphs representing these characters are widely available in a variety of fonts. Although these characters should meet almost all users needs, MathML recognizes that mathematics is not static and that new characters are added when convenient. Characters that become well accepted will likely be eventually incorporated by the Unicode Consortium or other standards bodies, but that is often a lengthy process. In the meantime, a mechanism is necessary for accessing glyphs from non-standard fonts representing these characters.
The mglyph element is the means by which
users can directly access glyphs for characters that are not defined
by Unicode, or not known to the renderer. Similarly, the mglyph element can also be used to select glyph
variants for existing Unicode characters, as might be desirable when a
glyph variant has begun to differentiate itself as a new character by
taking on a distinguished mathematical meaning.
The mglyph element names a specific
character glyph, and is valid inside any MathML leaf content listed in
Section 3.1.6 [Summary of Presentation Elements] (mi, etc.) or
Section 4.2.2 [Containers] (ci, etc.)
unless otherwise restricted by an attribute (e.g. base=2 to <cn>). In order
for a visually-oriented renderer to render the character, the renderer
must be told what font to use and what index within that font to
use.
mglyph elements accept the attributes listed in
Section 3.2.2 [Mathematics style attributes common to token
elements], and the additional attributes listed here.
| Name | values | default |
|---|---|---|
| alt | string | required |
| fontfamily | string | css-fontfamily | required |
| index | integer | required |
The alt attribute provides an alternate name
for the glyph. If the specified font can't be found, the renderer may
use this name in a warning message or some unknown glyph notation. The
name might also be used by an audio renderer or symbol processing
system and should be chosen to be descriptive. The fontfamily and index
uniquely identify the mglyph; two mglyphs with the same values for fontfamily and index should
be considered identical by applications that must determine whether
two characters/glyphs are identical. The alt
attribute should not be part of the identity test.
The fontfamily and index attributes name a font and position within
that font. All font properties apart from fontfamily are inherited. Variants of the font
(e.g., bold) that may be inherited may be ignored if the variant of
the font is not present.
Authors should be aware that rendering requires the fonts
referenced by mglyph, which the MathML
renderer may not have access to or may be not be supported by the
system on which the renderer runs. For these reasons, authors are
encouraged to use mglyph only when
absolutely necessary, and not for stylistic purposes.
The following example illustrates how a researcher might use the mglyph construct with an experimental font to work
with braid group notation.
<mrow> <mi><mglyph fontfamily="my-braid-font" index="2" alt="23braid"/></mi> <mo>+</mo> <mi><mglyph fontfamily="my-braid-font" index="5" alt="132braid"/></mi> <mo>=</mo> <mi><mglyph fontfamily="my-braid-font" index="3" alt="13braid"/></mi> </mrow>
This might render as:
Besides tokens there are several families of MathML presentation elements. One family of elements deals with various `scripting' notations, such as subscript and superscript. Another family is concerned with matrices and tables. The remainder of the elements, discussed in this section, describe other basic notations such as fractions and radicals, or deal with general functions such as setting style properties and error handling.
mrow)An mrow element is used to group together any
number of sub-expressions, usually consisting of one or more mo elements acting as `operators' on one
or more other expressions that are their `operands'.
Several elements automatically treat their arguments as if they were
contained in an mrow element. See the discussion of
inferred mrows in Section 3.1.3 [Required Arguments]. See also mfenced (Section 3.3.8 [Expression Inside Pair of Fences
(mfenced)]), which can effectively form an mrow containing its arguments separated by commas.
This element only permits id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
mrow elements are typically rendered visually
as a horizontal row of their arguments, left to right in the order in
which the arguments occur, or audibly as a sequence of renderings of
the arguments. The description in Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)] of suggested rendering
rules for mo elements assumes that all horizontal
spacing between operators and their operands is added by the rendering
of mo elements (or, more generally, embellished
operators), not by the rendering of the mrows
they are contained in.
MathML is designed to allow renderers to automatically linebreak expressions (that is, to break excessively long expressions into several lines), without requiring authors to specify explicitly how this should be done. This is because linebreaking positions can't be chosen well without knowing the width of the display device and the current font size, which for many uses of MathML will not be known except by the renderer at the time of each rendering.
Determining good positions for linebreaks is complex, and rules for
this are not described here; whether and how it is done is up to each
MathML renderer. Typically, linebreaking will involve selection of
`good' points for insertion of linebreaks between successive
arguments of mrow elements.
Although MathML does not require linebreaking or specify a
particular linebreaking algorithm, it has several features designed to
allow such algorithms to produce good results. These include the use
of special entities for certain operators, including invisible
operators (see Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)]), or for providing hints related to
linebreaking when necessary (see Section 3.2.6 [Text (mtext)]), and the ability to
use nested mrows to describe sub-expression
structure (see below).
mrow of one argumentMathML renderers are required to treat an mrow
element containing exactly one argument as equivalent in all ways to
the single argument occurring alone, provided there are no attributes
on the mrow element's start tag. If there are
attributes on the mrow element's start tag, no
requirement of equivalence is imposed. This equivalence condition is
intended to simplify the implementation of MathML-generating software
such as template-based authoring tools. It directly affects the
definitions of embellished operator and space-like element and the
rules for determining the default value of the form
attribute of an mo element;
see Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)] and Section 3.2.7 [Space (mspace)]. See also the discussion of equivalence of MathML
expressions in Chapter 7 [The MathML Interface].
mrow
Sub-expressions should be grouped by the document author in the same way
as they are grouped in the mathematical interpretation of the expression;
that is, according to the underlying `syntax tree' of the
expression. Specifically, operators and their mathematical arguments should
occur in a single mrow; more than one operator
should occur directly in one mrow only when they
can be considered (in a syntactic sense) to act together on the interleaved
arguments, e.g. for a single parenthesized term and its parentheses, for
chains of relational operators, or for sequences of terms separated by
+ and -. A precise rule is given below.
Proper grouping has several purposes: it improves display by possibly affecting spacing; it allows for more intelligent linebreaking and indentation; and it simplifies possible semantic interpretation of presentation elements by computer algebra systems, and audio renderers.
Although improper grouping will sometimes result in suboptimal
renderings, and will often make interpretation other than pure visual
rendering difficult or impossible, any grouping of expressions using
mrow is allowed in MathML syntax; that is,
renderers should not assume the rules for proper grouping will be
followed.
A precise rule for when and how to nest sub-expressions using
mrow is especially desirable when generating
MathML automatically by conversion from other formats for displayed
mathematics, such as TEX, which don't always specify how sub-expressions
nest. When a precise rule for grouping is desired, the following rule
should be used:
Two adjacent operators (i.e. mo elements,
possibly embellished), possibly separated by operands (i.e. anything
other than operators), should occur in the same
mrow only when the left operator has an infix or
prefix form (perhaps inferred), the right operator has an infix or
postfix form, and the operators are listed in the same group of
entries in the operator dictionary provided in Appendix F [Operator Dictionary].
In all other cases, nested mrows should be used.
When forming a nested mrow (during generation
of MathML) that includes just one of two successive operators with
the forms mentioned above (which mean that either operator could in
principle act on the intervening operand or operands), it is necessary
to decide which operator acts on those operands directly (or would do
so, if they were present). Ideally, this should be determined from the
original expression; for example, in conversion from an
operator-precedence-based format, it would be the operator with the
higher precedence. If this cannot be determined directly from the
original expression, the operator that occurs later in the suggested
operator dictionary (Appendix F [Operator Dictionary]) can be assumed to have
a higher precedence for this purpose.
Note that the above rule has no effect on whether any MathML expression is valid, only on the recommended way of generating MathML from other formats for displayed mathematics or directly from written notation.
(Some of the terminology used in stating the above rule in defined
in Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)].)
As an example, 2x+y-z should be written as:
<mrow>
<mrow>
<mn> 2 </mn>
<mo> ⁢ </mo>
<mi> x </mi>
</mrow>
<mo> + </mo>
<mi> y </mi>
<mo> - </mo>
<mi> z </mi>
</mrow>
The proper encoding of (x, y) furnishes a less obvious
example of nesting mrows:
<mrow>
<mo> ( </mo>
<mrow>
<mi> x </mi>
<mo> , </mo>
<mi> y </mi>
</mrow>
<mo> ) </mo>
</mrow>
In this case, a nested mrow is required inside
the parentheses, since parentheses and commas, thought of as fence and
separator `operators', do not act together on their arguments.
mfrac)The mfrac element is used for fractions. It can
also be used to mark up fraction-like objects such as binomial coefficients
and Legendre symbols. The syntax for mfrac is
<mfrac> numerator denominator </mfrac>
mfrac
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| linethickness | number [ v-unit ] | thin | medium | thick | 1 (rule thickness) |
| numalign | left | center | right | center |
| denomalign | left | center | right | center |
| bevelled | true | false | false |
The linethickness attribute indicates the thickness of
the horizontal `fraction bar', or `rule', typically used to render
fractions. A fraction with linethickness="0" renders
without the bar, and might be used within binomial coefficients. A
linethickness greater than one might be used with nested
fractions. These cases are shown below:
In general, the value of linethickness can be a
number, as a multiplier of the default thickness of the fraction bar
(the default thickness is not specified by MathML), or a number with a
unit of vertical length (see Section 2.4.4.2 [Attributes with units]), or one of the keywords
medium (same as 1), thin (thinner than 1,
otherwise up to the renderer), or thick (thicker than 1,
otherwise up to the renderer).
The numalign and
denomalign attributes control the horizontal
alignment of the numerator and denominator respectively. Typically,
numerators and denominators are centered, but a very long numerator or
denominator might be displayed on several lines and a left alignment
might be more appropriate for displaying them.
The bevelled attribute determines whether the
fraction is displayed with the numerator above the denominator
separated by a horizontal line or
whether a diagonal line is used to separate a slightly raised
numerator from a slightly lowered denominator. The latter form
corresponds to the attribute value being true
and provides for a more compact form for simple numerator and
denominators. An example illustrating the bevelled form is show below:
The mfrac element sets displaystyle to false, or if it
was already false increments scriptlevel by 1,
within numerator and denominator. These
attributes are inherited by every element from its rendering environment,
but can be set explicitly only on the mstyle
element. (See Section 3.3.4 [Style Change (mstyle)].)
The examples shown above can be represented in MathML as:
<mrow>
<mo> ( </mo>
<mfrac linethickness="0">
<mi> a </mi>
<mi> b </mi>
</mfrac>
<mo> ) </mo>
</mrow>
<mfrac linethickness="2">
<mfrac>
<mi> a </mi>
<mi> b </mi>
</mfrac>
<mfrac>
<mi> c </mi>
<mi> d </mi>
</mfrac>
</mfrac>
<mfrac>
<mn> 1 </mn>
<mrow>
<msup>
<mi> x </mi>
<mn> 3 </mn>
</msup>
<mo> + </mo>
<mfrac>
<mi> x </mi>
<mn> 3 </mn>
</mfrac>
</mrow>
</mfrac>
<mo> = </mo>
<mfrac bevelled="true">
<mn> 1 </mn>
<mrow>
<msup>
<mi> x </mi>
<mn> 3 </mn>
</msup>
<mo> + </mo>
<mfrac>
<mi> x </mi>
<mn> 3 </mn>
</mfrac>
</mrow>
</mfrac>
A more generic example is:
<mfrac>
<mrow>
<mn> 1 </mn>
<mo> + </mo>
<msqrt>
<mn> 5 </mn>
</msqrt>
</mrow>
<mn> 2 </mn>
</mfrac>
msqrt, mroot)These elements construct radicals. The msqrt element is
used for square roots, while the mroot element is used
to draw radicals with indices, e.g. a cube root. The syntax for these
elements is:
<msqrt> base </msqrt> <mroot> base index </mroot>
The mroot element requires exactly 2 arguments.
However, msqrt accepts any number of arguments; if
this number is not 1, its contents are treated as a single `inferred
mrow' containing its arguments, as described in
Section 3.1.3 [Required Arguments].
This element only permits id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
The mroot element increments scriptlevel by 2, and sets displaystyle to false, within
index, but leaves both attributes unchanged within
base. The msqrt element leaves both
attributes unchanged within all its arguments. These attributes are
inherited by every element from its rendering environment, but can be set
explicitly only on mstyle. (See Section 3.3.4 [Style Change (mstyle)].)
mstyle)The mstyle element is used to make style
changes that affect the rendering of its
contents. mstyle can be given any attribute
accepted by any MathML presentation element provided that the
attribute value is inherited, computed or has a default value;
presentation element attributes whose values are required are not
accepted by the mstyle element. In addition
mstyle can also be given certain special
attributes listed below.
The mstyle element accepts any number of
arguments. If this number is not 1, its contents are treated as a single
`inferred mrow' formed from all its
arguments, as described in Section 3.1.3 [Required Arguments].
Loosely speaking, the effect of the mstyle element
is to change the default value of an attribute for the elements it
contains. Style changes work in one of several ways, depending on
the way in which default values are specified for an attribute.
The cases are:
displaystyle or
scriptlevel (explained below), are inherited
from the surrounding context when they are not explicitly set. Specifying
such an attribute on an mstyle element sets the
value that will be inherited by its child elements. Unless a child element
overrides this inherited value, it will pass it on to its children, and
they will pass it to their children, and so on. But if a child element does
override it, either by an explicit attribute setting or automatically (as
is common for scriptlevel), the new (overriding)
value will be passed on to that element's children, and then to their
children, etc, until it is again overridden.
linethickness on
mfrac, have default values that are not normally
inherited. That is, if the linethickness attribute
is not set on the start tag of an mfrac element,
it will normally use the default value of 1, even if it was
contained in a larger mfrac element that set this
attribute to a different value. For attributes like this, specifying a
value with an mstyle element has the effect of
changing the default value for all elements within its scope. The net
effect is that setting the attribute value with mstyle propagates the change to all the elements it
contains directly or indirectly, except for the individual elements on
which the value is overridden. Unlike in the case of inherited attributes,
elements that explicitly override this attribute have no effect on this
attribute's value in their children.
stretchy and form, are
computed from operator dictionary information, position in the
enclosing mrow, and other similar data. For
these attributes, a value specified by an enclosing mstyle overrides the value that would normally be
computed.
Note that attribute values inherited from an
mstyle in any manner affect a given element
in the mstyle's content only if that attribute is
not given a value in that element's start tag. On any element for
which the attribute is set explicitly, the value specified on the
start tag overrides the inherited value. The only exception to this
rule is when the value given on the start tag is documented as
specifying an incremental change to the value inherited from that
element's context or rendering environment.
Note also that the difference between inherited and non-inherited
attributes set by mstyle, explained above, only
matters when the attribute is set on some element within the
mstyle's contents that has children also
setting it. Thus it never matters for attributes, such as
color, which can only be set on token elements (or on
mstyle itself).
There is one exceptional element, mpadded,
whose attributes cannot be set with mstyle.
The mpadded element shares several attribute
names with the mspace and mo elements. Thus, when the attributes width, height and depth are specified on an mstyle element, they apply only to the mspace element, and not the corresponding
attributes of mpadded. Similarly, when lspace is set with mstyle,
it applies only to the mo element.
As stated above, mstyle accepts all
attributes of all MathML presentation elements which do not have
required values. That is, all attributes which have an explicit
default value or a default value which is inherited or computed are
accepted by the mstyle element.
This element also accepts
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
Additionally, mstyle can be given the following special
attributes that are implicitly inherited by every MathML element as
part of its rendering environment:
| Name | values | default |
|---|---|---|
| scriptlevel | ['+' | '-'] unsigned-integer | inherited |
| displaystyle | true | false | inherited |
| scriptsizemultiplier | number | 0.71 |
| scriptminsize | number v-unit | 8pt |
| color | #rgb | #rrggbb | html-color-name | inherited |
| background | #rgb | #rrggbb | transparent | html-color-name | transparent |
| veryverythinmathspace | number h-unit | 0.0555556em |
| verythinmathspace | number h-unit | 0.111111em |
| thinmathspace | number h-unit | 0.166667em |
| mediummathspace | number h-unit | 0.222222em |
| thickmathspace | number h-unit | 0.277778em |
| verythickmathspace | number h-unit | 0.333333em |
| veryverythickmathspace | number h-unit | 0.388889em |
scriptlevel and displaystyle
MathML uses two attributes, displaystyle and
scriptlevel, to control orthogonal presentation features
that TEX encodes into one style attribute with values
\displaystyle, \textstyle, \scriptstyle, and \scriptscriptstyle. The
corresponding values of displaystyle and
scriptlevel for those TEX styles would be true and
0, false and
0, false and
1, and false and 2,
respectively.
The main effect of the displaystyle attribute is that
it determines the effect of other attributes such as the
largeop and movablescripts attributes of
mo. The main effect of the
scriptlevel attribute is to control the font
size. Typically, the higher the scriptlevel, the smaller
the font size. (Non-visual renderers can respond to the font size in
an analogous way for their medium.) More sophisticated renderers may
also choose to use these attributes in other ways, such as rendering
expressions with displaystyle=false in a more
vertically compressed manner.
These attributes are given initial values for the outermost expression of an instance of MathML based on its rendering environment. A short list of layout schemata described below modify these values for some of their sub-expressions. Otherwise, values are determined by inheritance whenever they are not directly specified on a given element's start tag.
For an instance of MathML embedded in a textual data format (such
as HTML) in `display' mode, i.e. in place of a paragraph,
displaystyle = true and
scriptlevel = 0 for the
outermost expression of the embedded MathML; if the
MathML is embedded in `inline' mode, i.e. in place of a character,
displaystyle = false and
scriptlevel = 0 for
the outermost expression. See Chapter 7 [The MathML Interface] for further
discussion of the distinction between `display' and `inline'
embedding of MathML and how this can be specified in particular
instances. In general, a MathML renderer may determine these initial
values in whatever manner is appropriate for the location and context
of the specific instance of MathML it is rendering, or if it has no
way to determine this, based on the way it is most likely to be used;
as a last resort it is suggested that it use the most generic values
displaystyle = "true" and
scriptlevel = "0".
The MathML layout schemata that typically display some of their
arguments in smaller type or with less vertical spacing, namely the
elements for scripts, fractions, radicals, and tables or matrices,
set displaystyle to false, and in some cases increase
scriptlevel, for those arguments. The new values are inherited
by all sub-expressions within those arguments, unless they are
overridden.
The specific rules by which each element modifies
displaystyle and/or scriptlevel are given in the
specification for each element that does so; the complete list of
elements that modify either attribute are: the `scripting' elements
msub, msup, msubsup,
munder, mover,
munderover, and mmultiscripts; and the
elements mfrac, mroot, and
mtable.
When mstyle is given a
scriptlevel attribute with no sign, it sets the value of
scriptlevel within its contents to the value given, which
must be a nonnegative integer. When the attribute value consists of a
sign followed by an integer, the value of scriptlevel is
incremented (for '+') or decremented (for '-') by the amount
given. The incremental syntax for this attribute is an exception to
the general rules for setting inherited attributes using
mstyle, and is not allowed by any other attribute
on mstyle.
Whenever the scriptlevel is changed, either
automatically or by being explicitly incremented, decremented, or set,
the current font size is multiplied by the value of
scriptsizemultiplier to the power of the change in
scriptlevel. For example, if scriptlevel is
increased by 2, the font size is multiplied by
scriptsizemultiplier twice in succession; if
scriptlevel is explicitly set to 2 when it had been 3,
the font size is divided by scriptsizemultiplier.
References to fontsize in this section should be
interpreted to mean either the fontsize attribute
or the mathsize attribute.
The default value of scriptsizemultiplier is less than
one (in fact, it is approximately the square root of 1/2), resulting
in a smaller font size with increasing scriptlevel. To
prevent scripts from becoming unreadably small, the font size is never
allowed to go below the value of scriptminsize as a
result of a change to scriptlevel, though it can be set
to a lower value using the fontsize attribute (Section 3.2.2 [Mathematics style attributes common to token
elements]) on mstyle or on token
elements. If a change to scriptlevel would cause the font
size to become lower than scriptminsize using the above
formula, the font size is instead set equal to
scriptminsize within the sub-expression for which
scriptlevel was changed.
In the syntax for scriptminsize, v-unit represents a unit of vertical length (as
described in Section 2.4.4.2 [Attributes with units]). The most common unit for specifying font sizes
in typesetting is pt (points).
Explicit changes to the fontsize attribute have no
effect on the value of scriptlevel.
scriptlevel for renderersFor MathML renderers that support CSS style sheets, or some other
analogous style sheet mechanism, absolute or relative changes to
fontsize (or other attributes) may occur implicitly on
any element in response to a style sheet. Changes to
fontsize of this kind also have no effect on
scriptlevel. A style sheet-induced change to
fontsize overrides scriptminsize in the same
way as for an explicit change to fontsize in the
element's start tag (discussed above), whether it is specified in the
style sheet as an absolute or a relative change. (However, any
subsequent scriptlevel-induced change to
fontsize will still be affected by it.) As is required
for inherited attributes in CSS, the style sheet-modified
fontsize is inherited by child elements.
If the same element is subject to both a style sheet-induced and an
automatic (scriptlevel-related) change to its own
fontsize, the scriptlevel-related change is
done first - in fact, in the simplest implementation of the
element-specific rules for scriptlevel, this change would
be done by the element's parent as part of producing the rendering
properties it passes to the given element, since it is the parent
element that knows whether scriptlevel should be changed
for each of its child elements.
If the element's own fontsize is changed by a style
sheet and it also changes scriptlevel (and thus
fontsize) for one of its children, the style
sheet-induced change is done first, followed by the change inherited
by that child. If more than one child's scriptlevel is
changed, the change inherited by each child has no effect on the other
children. (As a mnemonic rule that applies to a `parse tree' of
elements and their children, style sheet-induced changes to
fontsize can be associated to nodes of the tree, i.e. to
MathML elements, and scriptlevel-related changes can be
associated to the edges between parent and child elements; then the
order of the associated changes corresponds to the order of nodes and
edges in each path down the tree.) For general information on the
relative order of processing of properties set by style sheets versus by
attributes, see the appropriate subsection of CSS-compatible
attributes in Section 2.4.4.3 [CSS-compatible attributes].
If scriptlevel is changed incrementally by an
mstyle element that also sets certain other
attributes, the overall effect of the changes may depend on the order
in which they are processed. In such cases, the attributes in the
following list should be processed in the following order, regardless
of the order in which they occur in the XML-format attribute list of
the mstyle start tag:
scriptsizemultiplier, scriptminsize,
scriptlevel, fontsize.
Note that scriptlevel can, in principle, attain any
integral value by being decremented sufficiently, even though it can
only be explicitly set to nonnegative values. Negative values of
scriptlevel generated in this way are legal and should
work as described, generating font sizes larger than those of the
surrounding expression. Since scriptlevel is initially 0
and never decreases automatically, it will always be nonnegative
unless it is decremented past 0 using mstyle.
Explicit decrements of scriptlevel after the font size
has been limited by scriptminsize as described above
would produce undesirable results. This might occur, for example, in a
representation of a continued fraction, in which the scriptlevel was
decremented for part of the denominator back to its value for the
fraction as a whole, if the continued fraction itself was located in a
place that had a high scriptlevel. To prevent this
problem, MathML renderers should, when decrementing
scriptlevel, use as the initial font size the value the
font size would have had if it had never been limited by
scriptminsize. They should not, however, ignore the
effects of explicit settings of fontsize, even to values
below scriptminsize.
Since MathML renderers may be unable to make use of arbitrary font
sizes with good results, they may wish to modify the mapping from
scriptlevel to fontsize to produce better renderings in their
judgment. In particular, if fontsizes have to be rounded to available
values, or limited to values within a range, the details of how this
is done are up to the renderer. Renderers should, however, ensure that
a series of incremental changes to scriptlevel resulting in its
return to the same value for some sub-expression that it had in a
surrounding expression results in the same fontsize for that
sub-expression as for the surrounding expression.
Color and background attributes are discussed in Section 3.2.2.2 [Color-related attributes].
The suggested MathML visual rendering rules do not define the
precise extent of the region whose background is affected by using the
background attribute on mstyle,
except that, when mstyle's content does not have
negative dimensions and its drawing region is not overlapped by other
drawing due to surrounding negative spacing, this region should lie
behind all the drawing done to render the content of the
mstyle, but should not lie behind any of the
drawing done to render surrounding expressions. The effect of overlap
of drawing regions caused by negative spacing on the extent of the
region affected by the background attribute is not
defined by these rules.
The spacing between operators is often one of a small number of
potential values. MathML names these values and allows their values to
be changed. Because the default values for spacing around operators
that are given in the operator dictionary Appendix F [Operator Dictionary]
are defined using these named spaces, changing their values will produce
tighter or looser spacing. These values can be used anywhere a h-unit or v-unit unit is
allowed. See Section 2.4.4.2 [Attributes with units].
The predefined namedspaces are:
veryverythinmathspace,
verythinmathspace,
thinmathspace,
mediummathspace,
thickmathspace,
verythickmathspace, or
veryverythickmathspace.
The default values of veryverythinmathspace...
veryverythickmathspace are 1/18em...7/18em,
respectively.
The example of limiting the stretchiness of a parenthesis shown in the section on <mo>,
<mrow> <mo maxsize="1"> ( </mo> <mfrac> <mi> a </mi> <mi> b </mi> </mfrac> <mo maxsize="1"> ) </mo> </mrow>
can be rewritten using mstyle as:
<mstyle maxsize="1">
<mrow>
<mo> ( </mo>
<mfrac> <mi> a </mi> <mi> b </mi> </mfrac>
<mo> ) </mo>
</mrow>
</mstyle>
merror)The merror element displays its contents as an
`error message'. This might be done, for example, by displaying the
contents in red, flashing the contents, or changing the background
color. The contents can be any expression or expression sequence.
merror accepts any number of arguments; if
this number is not 1, its contents are treated as a single `inferred
mrow' as described in Section 3.1.3 [Required Arguments].
The intent of this element is to provide a standard way for programs that generate MathML from other input to report syntax errors in their input. Since it is anticipated that preprocessors that parse input syntaxes designed for easy hand entry will be developed to generate MathML, it is important that they have the ability to indicate that a syntax error occurred at a certain point. See Section 7.2.2 [Handling of Errors].
The suggested use of merror for reporting
syntax errors is for a preprocessor to replace the erroneous part of
its input with an merror element containing a
description of the error, while processing the surrounding expressions
normally as far as possible. By this means, the error message will be
rendered where the erroneous input would have appeared, had it been
correct; this makes it easier for an author to determine from the
rendered output what portion of the input was in error.
No specific error message format is suggested here, but as with
error messages from any program, the format should be designed to make
as clear as possible (to a human viewer of the rendered error message)
what was wrong with the input and how it can be fixed. If the
erroneous input contains correctly formatted subsections, it may be
useful for these to be preprocessed normally and included in the error
message (within the contents of the merror
element), taking advantage of the ability of
merror to contain arbitrary MathML expressions
rather than only text.
This element only permits id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
If a MathML syntax-checking preprocessor received the input
<mfraction> <mrow> <mn> 1 </mn> <mo> + </mo> <msqrt> <mn> 5 </mn> </msqrt> </mrow> <mn> 2 </mn> </mfraction>
which contains the non-MathML element mfraction
(presumably in place of the MathML element mfrac),
it might generate the error message
<merror>
<mtext> Unrecognized element: mfraction;
arguments were: </mtext>
<mrow> <mn> 1 </mn> <mo> + </mo> <msqrt> <mn> 5 </mn> </msqrt> </mrow>
<mtext> and </mtext>
<mn> 2 </mn>
</merror>
Note that the preprocessor's input is not, in this case, valid MathML, but the error message it outputs is valid MathML.
mpadded)An mpadded element renders the same as its
content, but with its overall size and other dimensions (such as
baseline position) modified according to its attributes. The
mpadded element does not rescale (stretch or
shrink) its content; its only effect is to modify the apparent size
and position of the `bounding box' around its content, so as to
affect the relative position of the content with respect to the
surrounding elements. The name of the element reflects the use of
mpadded to effectively add `padding', or extra
space, around its content. If the `padding' is negative, it is
possible for the content of mpadded to be
rendered outside the mpadded element's bounding
box; see below for warnings about several potential pitfalls of this
effect.
The mpadded element accepts any number of
arguments; if this number is not 1, its contents are treated as a single
`inferred mrow' as described in
Section 3.1.3 [Required Arguments].
It is suggested that audio renderers add (or shorten) time delays
based on the attributes representing horizontal space
(width and lspace).
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| width | [ + | - ] unsigned-number ( % [ pseudo-unit ] | pseudo-unit | h-unit | namedspace ) | same as content |
| lspace | [ + | - ] unsigned-number ( % [ pseudo-unit ] | pseudo-unit | h-unit ) | 0 |
| height | [ + | - ] unsigned-number ( % [ pseudo-unit ] | pseudo-unit | v-unit ) | same as content |
| depth | [ + | - ] unsigned-number ( % [ pseudo-unit ] | pseudo-unit | v-unit ) | same as content |
(The pseudo-unit syntax symbol is described below.)
These attributes modify the dimensions of the `bounding
box' of the mpadded element. The dimensions
(which have the same names as the attributes) are defined in the next
subsection. Depending on the format of the attribute value, a dimension
may be set to a new value, or to an incremented or decremented version of
the content's corresponding dimension. Values may be specified as multiples
or percentages of any of the dimensions of the normal rendering of the
element's content (using so-called `pseudo-units'), or
they can be set directly using standard units Section 2.4.4.2 [Attributes with units].
If an attribute value begins with a + or
- sign, it specifies an increment or decrement of the
corresponding dimension by the following length value (interpreted as
explained below). Otherwise, the corresponding dimension is set
directly to the following length value. Note that the +
and - do not mean that the following value is positive or
negative, even when an explicit length unit (h-unit or
v-unit) is given. In particular, these attributes cannot
directly set a dimension to a negative value.
Length values (after the optional sign, which is not part of the
length value) can be specified in several formats. Each format begins
with an unsigned-number, which may be followed by a
% sign and an optional `pseudo-unit' (denoted by
pseudo-unit in the attribute syntaxes above), by a
pseudo-unit alone, or by one of the length units
(denoted by h-unit or v-unit) specified in
Section 2.4.4.2 [Attributes with units], not including %. The possible
pseudo-units are the keywords width, lspace,
height, and depth; they each represent the
length of the same-named dimension of the mpadded
element's content (not of the mpadded element
itself). The lengths represented by h-unit or
v-unit are described in Section 2.4.4.2 [Attributes with units].
In any of these formats, the length value specified is the product
of the specified number and the length represented by the unit or
pseudo-unit. The result is multiplied by 0.01 if % is given. If no
pseudo-unit is given after %, the one with the same name
as the attribute being specified is assumed.
Some examples of attribute formats using pseudo-units (explicit or
default) are as follows: depth="100% height" and
depth="1.0 height" both set the depth of the
mpadded element to the height of its content.
depth="105%" sets the depth to 1.05 times the content's
depth, and either depth="+100%" or
depth="200%" sets the depth to twice the content's
depth.
Dimensions that would be positive if the content was rendered
normally cannot be made negative using mpadded; a
positive dimension is set to 0 if it would otherwise become negative.
Dimensions that are initially 0 can be made negative, but this
should generally be avoided. See the warnings below on the use of
negative spacing for `tweaking' or conveying meaning.
The rules given above imply that all of the following attribute settings have the same effect, which is to leave the content's dimensions unchanged:
<mpadded width="+0em"> ... </mpadded> <mpadded width="+0%"> ... </mpadded> <mpadded width="-0em"> ... </mpadded> <mpadded width="- 0 height"> ... </mpadded> <mpadded width="100%"> ... </mpadded> <mpadded width="100% width"> ... </mpadded> <mpadded width="1 width"> ... </mpadded> <mpadded width="1.0 width"> ... </mpadded> <mpadded> ... </mpadded>
See Appendix H [Glossary] for further information about some of the typesetting terms used here.
The width attribute refers to the overall horizontal
width of a bounding box. By default (i.e. when lspace is
not modified), the bounding box of the content of an
mpadded element should be rendered flush with the
left edge of the mpadded element's bounding
box. Thus, increasing width alone effectively adds space
on the right edge of the box.
The lspace attribute refers to the amount of space
between the left edge of a bounding box and the start of the rendering of its
contents' bounding box. Unlike the other dimensions,
lspace does not correspond to a real property of a
bounding box, but exists only transiently during the computations done
by each instance of mpadded. It is provided so
that there is a way to add space on the left edge of a bounding
box.
The rationale behind using width and
lspace to control horizontal padding instead of more
symmetric attributes, such as a hypothetical rspace and
lspace, is that it is desirable to have a `width' pseudo
unit, in part because `width' is an actual property of a bounding
box.
The height attribute refers to the amount of vertical
space between the baseline (the line along the bottom of most letter
glyphs in normal text rendering) and the top of the bounding box.
The depth attribute refers to the amount of vertical
space between the bottom of the bounding box and the baseline.
MathML renderers should ensure that, except for the effects of the
attributes, relative spacing between the contents of
mpadded and surrounding MathML elements is not
modified by replacing an mpadded element with an
mrow element with the same content. This holds
even if linebreaking occurs within the mpadded
element. However, if an mpadded element with
non-default attribute values is subjected to linebreaking, MathML does
not define how its attributes or rendering interact with the
linebreaking algorithm.
A likely temptation for the use of the mpadded
and mspace elements (and perhaps also mphantom and mtext) will be
for an author to improve the spacing generated by a specific renderer by
slightly modifying it in specific expressions, i.e. to
`tweak' the rendering.
Authors are strongly warned that different MathML renderers may use different spacing rules for computing the relative positions of rendered symbols in expressions that have no explicit modifications to their spacing; if renderer B improves upon renderer A's spacing rules, explicit spacing added to improve the output quality of renderer A may produce very poor results in renderer B, very likely worse than without any `tweaking' at all.
Even when a specific choice of renderer can be assumed, its spacing rules may be improved in successive versions, so that the effect of tweaking in a given MathML document may grow worse with time. Also, when style sheet mechanisms are extended to MathML, even one version of a renderer may use different spacing rules for users with different style sheets.
Therefore, it is suggested that MathML markup never use
mpadded or mspace elements
to tweak the rendering of specific expressions, unless the MathML is
generated solely to be viewed using one specific version of one MathML
renderer, using one specific style sheet (if style sheets are
available in that renderer).
In cases where the temptation to improve spacing proves too strong,
careful use of mpadded,
mphantom, or the alignment elements (Section 3.5.5 [Alignment Markers]) may give more portable results than the
direct insertion of extra space using mspace or
mtext. Advice given to the implementors of MathML
renderers might be still more productive, in the long run.
MathML elements that permit `negative spacing', namely
mspace, mpadded, and
mtext, could in theory be used to simulate new
notations or `overstruck' characters by the visual overlap of the
renderings of more than one MathML sub-expression.
This practice is strongly discouraged in all situations, for the following reasons:
More generally, any construct that uses spacing to convey mathematical meaning, rather than simply as an aid to viewing expression structure, is discouraged. That is, the constructs that are discouraged are those that would be interpreted differently by a human viewer of rendered MathML if all explicit spacing was removed.
If such constructs are used in spite of this warning, they should
be enclosed in a semantics element that also
provides an additional MathML expression that can be interpreted in a
standard way.
For example, the MathML expression
<mrow> <mpadded width="0"> <mi> C </mi> </mpadded> <mspace width="0.3em"/> <mtext> | </mtext> </mrow>
forms an overstruck symbol in violation of the policy stated above; it might be intended to represent the set of complex numbers for a MathML renderer that lacks support for the standard symbol used for this purpose. This kind of construct should always be avoided in MathML, for the reasons stated above; indeed, it should never be necessary for standard symbols, since a MathML renderer with no better method of rendering them is free to use overstriking internally, so that it can still support general MathML input.
However, if for whatever reason such a construct is used in MathML,
it should always be enclosed in a semantics element such as
<semantics>
<mrow>
<mpadded width="0"> <mi> C </mi> </mpadded>
<mspace width="0.3em"/>
<mtext> | </mtext>
</mrow>
<annotation-xml encoding="MathML-Presentation">
<mi> ℂ </mi>
</annotation-xml>
</semantics>
which provides an alternative, standard encoding for the desired symbol, which is much more easily interpreted than the construct using negative spacing. (The alternative encoding in this example uses MathML presentation elements; the content elements described in Chapter 4 [Content Markup] should also be considered.)
(The above warning also applies to most uses of rendering
attributes to alter the meaning conveyed by an expression, with the
exception of attributes on mi (such as
fontweight) used to distinguish one variable from
another.)
mphantom)The mphantom element renders invisibly, but
with the same size and other dimensions, including baseline position,
that its contents would have if they were rendered
normally. mphantom can be used to align parts of
an expression by invisibly duplicating sub-expressions.
The mphantom element accepts any number of
arguments; if this number is not 1, its contents are treated as a single
`inferred mrow' formed from all its
arguments, as described in Section 3.1.3 [Required Arguments].
This element only permits id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
Note that it is possible to wrap both an
mphantom and an mpadded
element around one MathML expression, as in
<mphantom><mpadded attribute-settings>
... </mpadded></mphantom>, to change its size and make it
invisible at the same time.
MathML renderers should ensure that the relative spacing between
the contents of an mphantom element and the
surrounding MathML elements is the same as it would be if the
mphantom element were replaced by an
mrow element with the same content. This holds
even if linebreaking occurs within the mphantom
element.
For the above reason, mphantom is
not considered space-like (Section 3.2.7 [Space (mspace)]) unless its
content is space-like, since the suggested rendering rules for
operators are affected by whether nearby elements are space-like. Even
so, the warning about the legal grouping of space-like elements may
apply to uses of mphantom.
There is one situation where the preceding rule for rendering an
mphantom may not give the desired effect. When an
mphantom is wrapped around a subsequence of the
arguments of an mrow, the default determination
of the form attribute for an mo
element within the subsequence can change. (See the default value of
the form attribute described in Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)].) It may be
necessary to add an explicit form attribute to such an
mo in these cases. This is illustrated in the
following example.
In this example, mphantom is used to ensure
alignment of corresponding parts of the numerator and denominator of a
fraction:
<mfrac>
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mrow>
<mi> x </mi>
<mphantom>
<mo form="infix"> + </mo>
<mi> y </mi>
</mphantom>
<mo> + </mo>
<mi> z </mi>
</mrow>
</mfrac>
This would render as something like
rather than as
The explicit attribute setting form="infix" on the
mo element inside the mphantom sets the
form attribute to what it would have been in the absence of the
surrounding mphantom. This is necessary since
otherwise, the + sign would be interpreted as a prefix
operator, which might have slightly different spacing.
Alternatively, this problem could be avoided without any explicit
attribute settings, by wrapping each of the arguments
<mo>+</mo> and <mi>y</mi> in its
own mphantom element, i.e.
<mfrac>
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mrow>
<mi> x </mi>
<mphantom>
<mo> + </mo>
</mphantom>
<mphantom>
<mi> y </mi>
</mphantom>
<mo> + </mo>
<mi> z </mi>
</mrow>
</mfrac>
mfenced)The mfenced element provides a convenient form
in which to express common constructs involving fences (i.e. braces,
brackets, and parentheses), possibly including separators (such as
comma) between the arguments.
For example, <mfenced> <mi>x</mi> </mfenced>
renders as `(x)' and is equivalent to
<mrow> <mo> ( </mo> <mi>x</mi> <mo> ) </mo> </mrow>
and
<mfenced> <mi>x</mi> <mi>y</mi> </mfenced>
renders as `(x, y)'
and is equivalent to
<mrow> <mo> ( </mo> <mrow> <mi>x</mi> <mo>,</mo> <mi>y</mi> </mrow> <mo> ) </mo> </mrow>
Individual fences or separators are represented using
mo elements, as described in Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)]. Thus, any mfenced
element is completely equivalent to an expanded form described below;
either form can be used in MathML, at the convenience of an author or
of a MathML-generating program. A MathML renderer is required to
render either of these forms in exactly the same way.
In general, an mfenced element can contain
zero or more arguments, and will enclose them between fences in an
mrow; if there is more than one argument, it will
insert separators between adjacent arguments, using an additional
nested mrow around the arguments and separators
for proper grouping (Section 3.3.1 [Horizontally Group Sub-Expressions
(mrow)]). The general expanded form is
shown below. The fences and separators will be parentheses and comma
by default, but can be changed using attributes, as shown in the
following table.
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| open | string | ( |
| close | string | ) |
| separators | character * | , |
A generic mfenced element, with all attributes
explicit, looks as follows:
<mfenced open="opening-fence"
close="closing-fence"
separators="sep#1 sep#2 ... sep#(n-1)" >
arg#1
...
arg#n
</mfenced>
The opening-fence and closing-fence are
arbitrary strings. (Since they are used as the content of
mo elements, any whitespace they contain will be
trimmed and collapsed as described in Section 2.4.6 [Collapsing Whitespace in Input].)
The value of separators is a sequence of zero or more
separator characters (or entity references), optionally separated by
whitespace. Each sep#i consists of exactly
one character or entity reference. Thus, separators=",;"
is equivalent to separators=" , ; ".
The general mfenced element shown above is
equivalent to the following expanded form:
<mrow>
<mo fence="true"> opening-fence </mo>
<mrow>
arg#1
<mo separator="true"> sep#1 </mo>
...
<mo separator="true"> sep#(n-1) </mo>
arg#n
</mrow>
<mo fence="true"> closing-fence </mo>
</mrow>
Each argument except the last is followed by a separator. The inner
mrow is added for proper grouping, as described in
Section 3.3.1 [Horizontally Group Sub-Expressions
(mrow)].
When there is only one argument, the above form has no separators;
since <mrow> arg#1 </mrow> is equivalent to
arg#1 (as described in Section 3.3.1 [Horizontally Group Sub-Expressions
(mrow)]), this case is also equivalent to:
<mrow> <mo fence="true"> opening-fence </mo> arg#1 <mo fence="true"> closing-fence </mo> </mrow>
If there are too many separator characters, the extra ones are
ignored. If separator characters are given, but there are too few, the
last one is repeated as necessary. Thus, the default value of
separators="," is equivalent to
separators=",,", separators=",,,", etc. If
there are no separator characters provided but some are needed, for
example if separators=" " or "" and there is more than
one argument, then no separator elements are inserted at all - that
is, the elements <mo separator="true"> sep#i
</mo> are left out entirely. Note that this is different
from inserting separators consisting of mo
elements with empty content.
Finally, for the case with no arguments, i.e.
<mfenced open="opening-fence"
close="closing-fence"
separators="anything" >
</mfenced>
the equivalent expanded form is defined to include just
the fences within an mrow:
<mrow> <mo fence="true"> opening-fence </mo> <mo fence="true"> closing-fence </mo> </mrow>
Note that not all `fenced expressions' can be encoded by an
mfenced element. Such exceptional expressions
include those with an `embellished' separator or fence or one
enclosed in an mstyle element, a missing or extra
separator or fence, or a separator with multiple content
characters. In these cases, it is necessary to encode the expression
using an appropriately modified version of an expanded form. As
discussed above, it is always permissible to use the expanded form
directly, even when it is not necessary. In particular, authors cannot
be guaranteed that MathML preprocessors won't replace occurrences of
mfenced with equivalent expanded forms.
Note that the equivalent expanded forms shown above include
attributes on the mo elements that identify them
as fences or separators. Since the most common choices of fences and
separators already occur in the operator dictionary with those
attributes, authors would not normally need to specify those
attributes explicitly when using the expanded form directly. Also, the
rules for the default form attribute (Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)])
cause the opening and closing fences to be effectively given the
values form="prefix" and form="postfix"
respectively, and the separators to be given the value
form="infix".
Note that it would be incorrect to use mfenced
with a separator of, for instance, `+', as an abbreviation for an
expression using `+' as an ordinary operator, e.g.
<mrow> <mi>x</mi> <mo>+</mo> <mi>y</mi> <mo>+</mo> <mi>z</mi> </mrow>
This is because the + signs would be treated as separators,
not infix operators. That is, it would render as if they were marked up as
<mo separator="true">+</mo>, which might therefore
render inappropriately.
(a+b)
<mfenced>
<mrow>
<mi> a </mi>
<mo> + </mo>
<mi> b </mi>
</mrow>
</mfenced>
Note that the above mrow is necessary so that
the mfenced has just one argument. Without it, this
would render incorrectly as `(a, +,
b)'.
[0,1)
<mfenced open="["> <mn> 0 </mn> <mn> 1 </mn> </mfenced>
f(x,y)
<mrow>
<mi> f </mi>
<mo> ⁡ </mo>
<mfenced>
<mi> x </mi>
<mi> y </mi>
</mfenced>
</mrow>
menclose)The menclose element renders its content
inside the enclosing notation specified by its notation attribute.
menclose accepts any number of arguments; if
this number is not 1, its contents are treated as a single `inferred
mrow' containing its arguments,
as described in Section 3.1.3 [Required Arguments].
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| notation | longdiv | actuarial | radical | longdiv |
When notation has the value longdiv, the contents are drawn enclosed by a long
division symbol. A complete example of long division is accomplished
by also using mtable and malign. When notation is
specified as actuarial, the contents are drawn
enclosed by an actuarial symbol. The case of notation=radical is
equivalent to the msqrt schema.
The following markup might be used to encode an elementary US-style long division problem.
<mtable columnspacing='0' rowspacing='0'>
<mtr>
<mtd></mtd>
<mtd columnalign='right'><mn>10</mn></mtd>
</mtr>
<mtr>
<mtd columnalign='right'><mn>131</mn></mtd>
<mtd columnalign='right'>
<menclose notation='longdiv'><mn>1413</mn></menclose>
</mtd>
</mtr>
<mtr>
<mtd></mtd>
<mtd columnalign='right'>
<mrow>
<munder>
<mn>131</mn>
<mo> _ </mo>
</munder>
<mphantom><mn>3</mn></mphantom>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd></mtd>
<mtd columnalign='right'><mn>103</mn></mtd>
</mtr>
</mtable>
This might be rendered roughly as:
An example of using menclose for actuarial
notation is
<msub>
<mi>a</mi>
<mrow>
<menclose notation='actuarial'>
<mi>n</mi>
</menclose>
<mo>⁢</mo>
<mi>i</mi>
</mrow>
</msub>
which renders roughly as
The elements described in this section position one or more scripts around a base. Attaching various kinds of scripts and embellishments to symbols is a very common notational device in mathematics. For purely visual layout, a single general-purpose element could suffice for positioning scripts and embellishments in any of the traditional script locations around a given base. However, in order to capture the abstract structure of common notation better, MathML provides several more specialized scripting elements.
In addition to sub/superscript elements, MathML has overscript
and underscript elements that place scripts above and below the base. These
elements can be used to place limits on large operators, or for placing
accents and lines above or below the base. The rules for rendering accents
differ from those for overscripts and underscripts, and this difference can
be controlled with the accent and accentunder attributes, as described in the appropriate
sections below.
Rendering of scripts is affected by the scriptlevel and displaystyle
attributes, which are part of the environment inherited by the rendering
process of every MathML expression, and are described under mstyle (Section 3.3.4 [Style Change (mstyle)]). These
attributes cannot be given explicitly on a scripting element, but can be
specified on the start tag of a surrounding mstyle
element if desired.
MathML also provides an element for attachment of tensor indices. Tensor indices are distinct from ordinary subscripts and superscripts in that they must align in vertical columns. Tensor indices can also occur in prescript positions.
Because presentation elements should be used to describe the abstract notational structure of expressions, it is important that the base expression in all `scripting' elements (i.e. the first argument expression) should be the entire expression that is being scripted, not just the rightmost character. For example, (x+y)2 should be written as:
<msup>
<mrow>
<mo> ( </mo>
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
</mrow>
<mo> ) </mo>
</mrow>
<mn> 2 </mn>
</msup>
msub)The syntax for the msub element is:
<msub> base subscript </msub>
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| subscriptshift | number v-unit | automatic (typical unit is ex) |
The subscriptshift attribute specifies the minimum
amount to shift the baseline of subscript down.
v-unit represents a unit of vertical length (see Section 2.4.4.2 [Attributes with units]).
The msub element increments
scriptlevel by 1, and sets displaystyle to
false, within subscript, but leaves both attributes
unchanged within base. (These attributes are inherited by
every element through its rendering environment, but can be set
explicitly only on mstyle; see Section 3.3.4 [Style Change (mstyle)].)
msup)The syntax for the msup element is:
<msup> base superscript </msup>
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| superscriptshift | number v-unit | automatic (typical unit is ex) |
The superscriptshift attribute specifies the
minimum amount to shift the baseline of superscript up.
v-unit represents a unit of vertical length (see Section 2.4.4.2 [Attributes with units]).
The msup element increments scriptlevel by 1, and sets displaystyle to false, within
superscript, but leaves both attributes unchanged within
base. (These attributes are inherited by every element through
its rendering environment, but can be set explicitly only on mstyle; see Section 3.3.4 [Style Change (mstyle)].)
msubsup)The msubsup element is used to attach both a subscript and
superscript to a base expression. Note that both scripts are
positioned tight against the base:
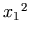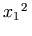 versus
versus
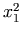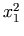 .
.
The syntax for the msubsup element is:
<msubsup> base subscript superscript </msubsup>
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| subscriptshift | number v-unit | automatic (typical unit is ex) |
| superscriptshift | number v-unit | automatic (typical unit is ex) |
The subscriptshift attribute specifies the minimum
amount to shift the baseline of subscript down. The
superscriptshift attribute specifies the minimum amount
to shift the baseline of superscript up.
v-unit represents a unit of vertical length (see Section 2.4.4.2 [Attributes with units]).
The msubsup element increments
scriptlevel by 1, and sets displaystyle to
false, within subscript and superscript,
but leaves both attributes unchanged within base. (These
attributes are inherited by every element through its rendering
environment, but can be set explicitly only on
mstyle; see Section 3.3.4 [Style Change (mstyle)].)
The msubsup is most commonly used for adding
sub/superscript pairs to identifiers as illustrated above. However,
another important use is placing limits on certain large operators
whose limits are traditionally displayed in the script positions even
when rendered in display style. The most common of these is the
integral. For example,
would be represented as
<mrow>
<msubsup>
<mo> ∫ </mo>
<mn> 0 </mn>
<mn> 1 </mn>
</msubsup>
<mrow>
<msup>
<mi> ⅇ </mi>
<mi> x </mi>
</msup>
<mo> ⁢ </mo>
<mrow>
<mo> ⅆ </mo>
<mi> x </mi>
</mrow>
</mrow>
</mrow>
munder)The syntax for the munder element is:
<munder> base underscript </munder>
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| accentunder | true | false | automatic |
The accentunder attribute controls whether
underscript is drawn as an `accent' or as a limit. The
main difference between an accent and a limit is that the limit is
reduced in size whereas an accent is the same size as the base. A
second difference is that the accent is drawn closer to the base.
The default value of accentunder is false, unless
underscript is an mo element or an
embellished operator (see Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)]). If
underscript is an mo element, the
value of its accent attribute is used as the default
value of accentunder. If underscript is an
embellished operator, the accent attribute of the
mo element at its core is used as the default
value. As with all attributes, an explicitly given value overrides
the default.
Here is an example (accent versus underscript):
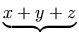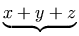 versus
versus
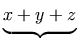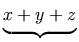 .
The MathML representation for this example is shown below.
.
The MathML representation for this example is shown below.
If the base is an operator with movablelimits=true (or an embellished operator whose mo element core has movablelimits=true), and displaystyle=false, then
underscript is drawn in a subscript position. In this case,
the accentunder attribute is ignored. This is often
used for limits on symbols such as ∑.
Within underscript, munder always
sets displaystyle to false, but increments
scriptlevel by 1 only when accentunder is
false. Within base, it always leaves both attributes
unchanged. (These attributes are inherited by every element through
its rendering environment, but can be set explicitly only on
mstyle; see Section 3.3.4 [Style Change (mstyle)].)
The MathML representation for the example shown above is:
<mrow>
<munder accentunder="true">
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mo> ⏟ </mo>
</munder>
<mtext> versus </mtext>
<munder accentunder="false">
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mo> ⏟ </mo>
</munder>
</mrow>
mover)The syntax for the mover element is:
<mover> base overscript </mover>
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| accent | true | false | automatic |
The accent attribute controls whether
overscript is drawn as an `accent' (diacritical mark) or
as a limit. The main difference between an accent and a limit is that
the limit is reduced in size whereas an accent is the same size as the
base. A second difference is that the accent is drawn closer to the
base. This is shown below (accent versus limit):
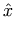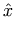 versus
versus
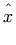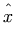 .
.
These differences also apply to `mathematical accents' such as
bars over expressions:
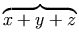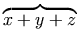 versus
versus
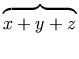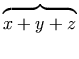 .
The MathML representation for each of these examples is shown below.
.
The MathML representation for each of these examples is shown below.
The default value of accent is false, unless
overscript is an mo element or an
embellished operator (see Section 3.2.5 [Operator, Fence, Separator or Accent
(mo)]). If
overscript is an mo element, the value
of its accent attribute is used as the default value
of accent for mover. If
overscript is an embellished operator, the accent attribute of the mo
element at its core is used as the default value.
If the base is an operator with movablelimits=true (or an embellished operator whose mo element core has movablelimits=true), and displaystyle=false, then
overscript is drawn in a superscript position. In this case,
the accent attribute is ignored. This is often used
for limits on symbols such as ∑.
Within overscript, mover always
sets displaystyle to false,
but increments scriptlevel by 1 only when accent is false. Within
base, it always leaves both attributes unchanged. (These
attributes are inherited by every element through its rendering
environment, but can be set explicitly only on mstyle; see Section 3.3.4 [Style Change (mstyle)].)
The MathML representation for the examples shown above is:
<mrow>
<mover accent="true">
<mi> x </mi>
<mo> ^ </mo>
</mover>
<mtext> versus </mtext>
<mover accent="false">
<mi> x </mi>
<mo> ^ </mo>
</mover>
</mrow>
<mrow>
<mover accent="true">
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mo> ‾ </mo>
</mover>
<mtext> versus </mtext>
<mover accent="false">
<mrow>
<mi> x </mi>
<mo> + </mo>
<mi> y </mi>
<mo> + </mo>
<mi> z </mi>
</mrow>
<mo> ‾ </mo>
</mover>
</mrow>
munderover)The syntax for the munderover element is:
<munderover> base underscript overscript </munderover>
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| accent | true | false | automatic |
| accentunder | true | false | automatic |
The munderover element is used so that the
underscript and overscript are vertically spaced equally in relation
to the base and so that they follow the slant of the base as in the
second expression shown below:
versus
The MathML representation for this example is shown below.
The difference in the vertical spacing is too small to be noticed on a low resolution display at a normal font size, but is noticeable on a higher resolution device such as a printer and when using large font sizes. In addition to the visual differences, attaching both the underscript and overscript to the same base more accurately reflects the semantics of the expression.
The accent and accentunder
attributes have the same effect as the attributes with the same names on
mover (Section 3.4.5 [Overscript (mover)]) and munder (Section 3.4.4 [Underscript (munder)]),
respectively. Their default values are also computed in the same manner as
described for those elements, with the default value of accent depending on overscript and the
default value of accentunder depending on
underscript.
If the base is an operator with movablelimits=true (or an embellished operator whose mo element core has movablelimits=true), and displaystyle=false, then
underscript and overscript are drawn in a
subscript and superscript position, respectively. In this case, the accent and accentunder attributes
are ignored. This is often used for limits on symbols such as ∑.
Within underscript, munderover
always sets displaystyle to false, but increments scriptlevel
by 1 only when accentunder is false. Within overscript, munderover always sets displaystyle to false, but
increments scriptlevel by 1 only when accent is false. Within
base, it always leaves both attributes unchanged. (These
attributes are inherited by every element through its rendering
environment, but can be set explicitly only on mstyle; see Section 3.3.4 [Style Change (mstyle)]).
The MathML representation for the example shown above with the first
expression made using separate munder and
mover elements, and the second one using an
munderover element, is:
<mrow>
<mover>
<munder>
<mo> ∫ </mo>
<mn> 0 </mn>
</munder>
<mi> ∞ </mi>
</mover>
<mtext> versus </mtext>
<munderover>
<mo> ∫ </mo>
<mn> 0 </mn>
<mi> ∞ </mi>
</munderover>
</mrow>
mmultiscripts)The syntax for the mmultiscripts element is:
<mmultiscripts>
base
(subscript superscript)*
[ <mprescripts/> (presubscript presuperscript)* ]
</mmultiscripts>
Presubscripts and tensor notations are represented by a single
element, mmultiscripts. This element allows the
representation of any number of vertically-aligned pairs of subscripts
and superscripts, attached to one base expression. It supports both
postscripts (to the right of the base in visual notation) and
prescripts (to the left of the base in visual notation). Missing
scripts can be represented by the empty element
none.
The prescripts are optional, and when present are given after the postscripts, because prescripts are relatively rare compared to tensor notation.
The argument sequence consists of the base followed by zero or more
pairs of vertically-aligned subscripts and superscripts (in that
order) that represent all of the postscripts. This list is optionally
followed by an empty element mprescripts and a
list of zero or more pairs of vertically-aligned presubscripts and
presuperscripts that represent all of the prescripts. The pair lists
for postscripts and prescripts are given in a left-to-right order. If
no subscript or superscript should be rendered in a given position,
then the empty element none should be used in
that position.
The base, subscripts, superscripts, the optional separator element
mprescripts, the presubscripts, and the
presuperscripts, are all direct sub-expressions of the
mmultiscripts element, i.e. they are all at the
same level of the expression tree. Whether a script argument is a
subscript or a superscript, or whether it is a presubscript or a
presuperscript is determined by whether it occurs in an even-numbered
or odd-numbered argument position, respectively, ignoring the empty
element mprescripts itself when determining the
position. The first argument, the base, is considered to be in
position 1. The total number of arguments must be odd, if
mprescripts is not given, or even, if it is.
The empty elements mprescripts and
none are only allowed as direct sub-expressions
of mmultiscripts.
Same as the attributes of msubsup.
The mmultiscripts element increments scriptlevel by 1, and sets displaystyle to false, within
each of its arguments except base, but leaves both attributes
unchanged within base. (These attributes are inherited by
every element through its rendering environment, but can be set explicitly
only on mstyle; see Section 3.3.4 [Style Change (mstyle)].)
Two examples of the use of mmultiscripts are:
0F1(;a;z).
<mrow>
<mmultiscripts>
<mi> F </mi>
<mn> 1 </mn>
<none/>
<mprescripts/>
<mn> 0 </mn>
<none/>
</mmultiscripts>
<mo> ⁡ </mo>
<mrow>
<mo> ( </mo>
<mrow>
<mo> ; </mo>
<mi> a </mi>
<mo> ; </mo>
<mi> z </mi>
</mrow>
<mo> ) </mo>
</mrow>
</mrow>
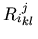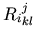 (where k and l are different indices)
(where k and l are different indices)
<mmultiscripts> <mi> R </mi> <mi> i </mi> <none/> <none/> <mi> j </mi> <mi> k </mi> <none/> <mi> l </mi> <none/> </mmultiscripts>
Matrices, arrays and other table-like mathematical notation are marked
up using mtable,
mtr, mlabeledtr and
mtd elements. These elements are similar to the
TABLE, TR and TD elements of HTML, except that they provide
specialized attributes for the fine layout control
necessary for commutative diagrams, block matrices and so on.
The mlabeledtr element represents a labeled
row of a table and can be used for numbered equations.
The first child of mlabeledtr is the label.
A label is somewhat special in that it is not considered an expression
in the matrix and is not counted when determining the number of columns
in that row.
mtable)A matrix or table is specified using the mtable element. Inside of the mtable element, only mtr
or mlabeledtr elements may appear.
In MathML 1.x, the mtable element could
infer mtr elements around its arguments, and
the mtr element could infer mtd elements. In other words, if some argument to
an mtable was not an mtr element, a MathML application was to assume a
row with a single column (i.e. the argument was effectively wrapped
with an inferred mtr). Similarly, if some
argument to a (possibly inferred) mtr element
was not an mtd element, that argument was to
be treated as a table entry by wrapping it with an inferred mtd element.
MathML 2.0 deprecates the inference
of mtr and mtd elements;
mtr and mtd elements
must be used inside of mtable and
mtr respectively.
Table rows that have fewer columns than other rows of the same
table (whether the other rows precede or follow them) are effectively
padded on the right with empty mtd elements so
that the number of columns in each row equals the maximum number of
columns in any row of the table. Note that the use of
mtd elements with non-default values of the
rowspan or columnspan
attributes may affect
the number of mtd elements that should be given
in subsequent mtr elements to cover a given
number of columns.
Note also that the label in an mlabeledtr element
is not considered a column in the table.
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| align | (top | bottom | center | baseline | axis) [ rownumber ] | axis |
| rowalign | (top | bottom | center | baseline | axis) + | baseline |
| columnalign | (left | center | right) + | center |
| groupalign | group-alignment-list-list | {left} |
| alignmentscope | (true | false) + | true |
| columnwidth | ( auto | number h-unit | namedspace | fit ) + | auto |
| width | auto | number h-unit | auto |
| rowspacing | ( number v-unit ) + | 1.0ex |
| columnspacing | ( number h-unit | namedspace ) + | 0.8em |
| rowlines | (none | solid | dashed) + | none |
| columnlines | (none | solid | dashed) + | none |
| frame | none | solid | dashed | none |
| framespacing | (number h-unit | namedspace) (number v-unit | namedspace) | 0.4em 0.5ex |
| equalrows | true | false | false |
| equalcolumns | true | false | false |
| displaystyle | true | false | false |
| side | left | right | leftoverlap | rightoverlap | right |
| minlabelspacing | number h-unit | 0.8em |
Note that the default value for each of rowlines, columnlines and
frame is the literal string
`none', meaning that the default is to render no lines,
rather than that there is no default.
As described in Section 2.4.4 [MathML Attribute Values], the notation (x
| y)+ means one or more occurrences of either x or
y, separated by whitespace. For example, possible values
for columnalign are left, left left, and left right center center. If there are more
entries than are necessary (e.g. more entries than columns for columnalign), then only the first entries will be
used. If there are fewer entries, then the last entry is repeated as
often as necessary. For example, if columnalign="right center" and the table has three
columns, the first column will be right aligned and the second and
third columns will be centered. The label in a mlabeledtr is not considered as a column in the
table and the attribute values that apply to columns do not apply to
labels.
The align attribute specifies where to align the
table with respect to its environment. axis means to align
the center of the table on the environment's axis. (The axis of an equation
is an alignment line used by typesetters. It is the line on which a minus
sign typically lies. The center of the table is the midpoint of the
table's vertical extent.) center and baseline
both mean to align the center of the table on the environment's
baseline. top or bottom aligns the top or
bottom of the table on the environment's baseline.
If the align attribute value ends with a
rownumber between 1 and n (for a table with
n rows), the specified row is aligned in the way described above,
rather than the table as a whole; the top (first) row is numbered 1, and
the bottom (last) row is numbered n. The same is true if the
row number is negative, between -1 and -n,
except that the bottom row is referred to as -1 and the top row as
-n. Other values of rownumber are
illegal.
The rowalign attribute specifies how the entries in
each row should be aligned. For example, top means that the tops of
each entry in each row should be aligned with the tops of the other
entries in that row. The columnalign attribute specifies
how the entries in each column should be aligned.
The groupalign and alignmentscope
attributes are described with the alignment elements,
maligngroup and
malignmark, in Section 3.5.5 [Alignment Markers].
The columnwidth attribute specifies how wide
a column should be. The auto value means that
the column should be as wide as needed, which is the default. If an
explicit value is given, then the column is exactly that wide and the
contents of that column are made to fit in that width. The contents
are linewrapped or clipped at the discretion of the renderer. If fit is given as a value, the remaining page width
after subtracting the widths for columns specified as auto and/or specific widths is divided equally
among the fit columns and this value is used
for the column width. If insufficient room remains to hold the
contents of the fit columns, renderers may
linewrap or clip the contents of the fit
columns. When the columnwidth is specified as
a percentage, the value is relative to the width of the table. That
is, a renderer should try to adjust the width of the column so that it
covers the specified percentage of the entire table width.
The width attribute specifies the desired
width of the entire table and is intended for visual user agents. When
the value is a percentage value, the value is relative to the
horizontal space a MathML renderer has available for the table
element. When the value is auto, the MathML
renderer should calculate the table width from its contents using
whatever layout algorithm it chooses.
MathML 2.0 does not specify a table layout algorithm. In
particular, it is the responsibility of a MathML renderer to resolve
conflicts between the width attribute and other
constraints on the width of a table, such as explicit values for columnwidth attributes, and minimum sizes for table
cell contents. For a discussion of table layout algorithms, see
Cascading
Style Sheets, level 2.
The rowspacing and columnspacing
attributes specify how much space should be added between each row and
column. However, spacing before the first row and after the last row
(i.e. at the top and bottom of the table) is given by the second
number in the value of the framespacing attribute, and
spacing before the first column and after the last column (i.e. on the
left and on the right of the table) is given by the first number in
the value of the framespacing attribute.
In those attributes' syntaxes, h-unit or
v-unit represents a unit of horizontal or vertical
length, respectively (see Section 2.4.4.2 [Attributes with units]). The units shown in the
attributes' default values (em or ex) are
typically used.
The rowlines and columnlines attributes
specify whether and what kind of lines should be added between each
row and column. Lines before the first row or column and after the
last row or column are given using the frame
attribute.
If a frame is desired around the table, the frame
attribute is used. If the attribute value is not `none', then
framespacing is used to add spacing between the lines of
the frame and the first and last rows and columns of the table. If
frame="none", then the framespacing
attribute is ignored. The frame and
framespacing attributes are not part of the
rowlines/columnlines,
rowspacing/columnspacing options because
having them be so would often require that rowlines and
columnlines would need to be fully specified instead of
just giving a single value.
For example, if a table had five columns and it was desired to have
no frame around the table but to have lines between the columns, then
columnlines="none solid solid solid solid none"
would be necessary. If the frame is separated from the internal
lines, only columnlines="solid" is needed.
The equalrows attribute forces the rows all to be
the same total height when set to true. The equalcolumns attribute forces the columns all to be the
same width when set to true.
The displaystyle attribute specifies the
value of displaystyle (described under mstyle in Section 3.3.4 [Style Change (mstyle)]) within
each cell (mtd element) of the table. Setting
displaystyle=true can be
useful for tables whose elements are whole mathematical expressions;
the default value of false is appropriate when
the table is part of an expression, for example, when it represents a
matrix. In either case, scriptlevel (Section 3.3.4 [Style Change (mstyle)]) is not changed for the table cells.
The side attribute
specifies what side of a table a label for a table row should should be
placed. This attribute is intended to be used for labeled expressions.
If left or right is specified,
the label is placed on the left or right side of the table row respectively.
The other two attribute values are variations on
left and right:
if the labeled row fits within the width allowed for the table without
the label,
but does not fit within the width if the label is included, then the
label overlaps the row and is displayed above the row if
rowalign for that row is top;
otherwise the label is displayed below the row.
If there are multiple labels in a table, the alignment of the labels within
the virtual column that they form is left-aligned for labels on the left
side of the table, and right-aligned for labels on the right side of the
table. The alignment can be overridden by specifying
columnalignment for a mlabeledtr
element.
The minlabelspacing attribute
specifies the minimum space allowed between a label and the adjacent
entry in the row.
A 3 by 3 identity matrix could be represented as follows:
<mrow>
<mo> ( </mo>
<mtable>
<mtr>
<mtd> <mn>1</mn> </mtd>
<mtd> <mn>0</mn> </mtd>
<mtd> <mn>0</mn> </mtd>
</mtr>
<mtr>
<mtd> <mn>0</mn> </mtd>
<mtd> <mn>1</mn> </mtd>
<mtd> <mn>0</mn> </mtd>
</mtr>
<mtr>
<mtd> <mn>0</mn> </mtd>
<mtd> <mn>0</mn> </mtd>
<mtd> <mn>1</mn> </mtd>
</mtr>
</mtable>
<mo> ) </mo>
</mrow>
This might be rendered as:
Note that the parentheses must be represented explicitly; they are not
part of the mtable element's rendering. This allows
use of other surrounding fences, such as brackets, or none at all.
mtr)An mtr element represents one row in a table
or matrix. An mtr element is only allowed as a
direct sub-expression of an mtable element, and
specifies that its contents should form one row of the table. Each
argument of mtr is placed in a different column
of the table, starting at the leftmost column.
As described in Section 3.5.1 [Table or Matrix
(mtable)],
mtr elements are
effectively padded on the right with mtd
elements when they are shorter than other rows in a table.
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| rowalign | top | bottom | center | baseline | axis | inherited |
| columnalign | (left | center | right) + | inherited |
| groupalign | group-alignment-list-list | inherited |
The rowalign and columnalign attributes allow a specific row to
override the alignment specified by the same attributes in the
surrounding mtable element.
As with mtable, if there are more entries than
necessary in the value of columnalign (i.e. more entries
than columns in the row), then the extra entries will be ignored. If
there are fewer entries than columns, then the last entry will be
repeated as many times as needed.
The groupalign attribute is described with the alignment
elements, maligngroup and malignmark,
in Section 3.5.5 [Alignment Markers].
mlabeledtr)An mlabeledtr element represents one row in
a table that has a label on either the left or right side, as
determined by the side attribute. The label is
the first child of mlabeledtr. The rest of
the children represent the contents of the row and are identical to
those used for mtr; all of the children except
the first must be mtd elements.
An mlabeledtr element is only allowed as a
direct sub-expression of an mtable element.
Each argument of mlabeledtr except for the first
argument (the label) is placed in a different column
of the table, starting at the leftmost column.
Note that the label element is not considered to be a cell in the
table row. In particular, the label element is not taken into
consideration in the table layout for purposes of width and alignment
calculations. For example, in the case of an mlabeledtr with a label and a single centered mtd child, the child is first centered in the
enclosing mtable, and then the label is
placed. Specifically, the child is not centered in the
space that remains in the table after placing the label.
While MathML 2.0 does not specify an algorithm for placing labels,
implementors of visual renderers may find the following formatting
model useful. To place a label, an implementor might think in terms
of creating a larger table, with an extra column on both ends. The
columnwidth attributes of both these border
columns would be set to fit so that they expand
to fill whatever space remains after the inner columns have been laid
out. Finally, depending on the values of side
and minlabelspacing, the label is placed
in whatever border column is appropriate, possibly shifted down if
necessary.
The attributes for mlabeledtr are the same
as for mtr. Unlike the attributes for the
mtable element, attributes of
mlabeledtr that apply to column elements
also apply to the label. For example, in a one column table,
<mlabeledtr rowalign='top'>
means that the label and other entries in the row are vertically aligned
along their top. To force a particular alignment on the label,
the appropriate attribute would normally be set on the
mtd start tag that surrounds the label content.
One of the important uses of mlabeledtr is
for numbered equations. In a mlabeledtr, the
label represents the equation number and the elements in the row are
the equation being numbered. The side and minlabelspacing attributes of mtable determine the placement of the equation
number.
In larger documents with many numbered equations, automatic
numbering becomes important. While automatic equation numbering and
automatically resolving references to equation numbers is outside the
scope of MathML, these problems can be addressed by the use of style
sheets or other means. The mlabeledtr construction provides support
for both of these functions in a way that is intended to facilitate
XSLT processing. The mlabeledtr element can be
used to indicate the presence of a numbered equation, and the first
child can be changed to the current equation number, along with
incrementing the global equation number. For cross references, an
id on either the mlabeledtr element or on the first element
itself could be used as a target of any link.
<mtable>
<mlabeledtr id='e-is-m-c-square'>
<mtd>
<mtext> (2.1) </mtext>
</mtd>
<mtd>
<mrow>
<mi>E</mi>
<mo>=</mo>
<mrow>
<mi>m</mi>
<mo>⁢</mo>
<msup>
<mi>c</mi>
<mn>2</mn>
</msup>
</mrow>
</mrow>
</mtd>
</mlabeledtr>
</mtable>
This should be rendered as:
| E = mc2 | (2.1) |
mtd)An mtd element represents one entry, or cell, in a
table or matrix. An mtd element is only
allowed as a direct sub-expression of an mtr
or an mlabeledtr element.
The mtd element accepts any number of
arguments; if this number is not 1, its contents are treated as a single
`inferred mrow' formed from all its
arguments, as described in Section 3.1.3 [Required Arguments].
| Name | values | default |
|---|---|---|
| rowspan | number | 1 |
| columnspan | number | 1 |
| rowalign | top | bottom | center | baseline | axis | inherited |
| columnalign | left | center | right | inherited |
| groupalign | group-alignment-list | inherited |
The rowspan and columnspan attributes
allow a specific matrix element to be treated as if it occupied the
number of rows or columns specified. The interpretation of how this
larger element affects specifying subsequent rows and columns is meant
to correspond with the similar attributes for HTML 4.01 tables.
The rowspan and columnspan attributes
can be used around an mtd element that represents
the label in a mlabeledtr element.
Also, the label of a mlabeledtr element is not
considered to be part of a previous rowspan and
columnspan.
The rowalign and columnalign attributes
allow a specific matrix element to override the alignment specified by
a surrounding mtable or mtr
element.
The groupalign attribute is described with the alignment
elements, maligngroup and malignmark,
in Section 3.5.5 [Alignment Markers].
Alignment markers are space-like elements (see Section 3.2.7 [Space (mspace)]) that can be used
to vertically align specified points within a column of MathML
expressions by the automatic insertion of the necessary amount of
horizontal space between specified sub-expressions.
The discussion that follows will use the example of a set of simultaneous equations that should be rendered with vertical alignment of the coefficients and variables of each term, by inserting spacing somewhat like that shown here:
8.44x + 55 y = 0
3.1 x - 0.7y = -1.1
If the example expressions shown above were arranged in a column but not aligned, they would appear as:
8.44x + 55y = 0
3.1x - 0.7y = -1.1
(For audio renderers, it is suggested that the alignment elements produce the analogous behavior of altering the rhythm of pronunciation so that it is the same for several sub-expressions in a column, by the insertion of the appropriate time delays in place of the extra horizontal spacing described here.)
The expressions whose parts are to be aligned (each equation, in the
example above) must be given as the table elements (i.e. as the mtd elements) of one column of an
mtable. To avoid confusion, the term `table
cell' rather than `table element' will be used in the
remainder of this section.
All interactions between alignment elements are limited to the
mtable column they arise in. That is, every
column of a table specified by an mtable element
acts as an `alignment scope' that contains within it all alignment
effects arising from its contents. It also excludes any interaction
between its own alignment elements and the alignment elements inside
any nested alignment scopes it might contain.
The reason mtable columns are used as
alignment scopes is that they are the only general way in MathML to
arrange expressions into vertical columns. Future versions of MathML
may provide an malignscope element that allows
an alignment scope to be created around any MathML element, but even
then, table columns would still sometimes need to act as alignment
scopes, and since they are not elements themselves, but rather are
made from corresponding parts of the content of several
mtr elements, they could not individually be the
content of an alignment scope element.
An mtable element can be given the attribute
alignmentscope=false to cause
its columns not to act as alignment scopes. This is discussed further at
the end of this section. Otherwise, the discussion in this section assumes
that this attribute has its default value of true.
To cause alignment, it is necessary to specify, within each
expression to be aligned, the points to be aligned with corresponding
points in other expressions, and the beginning of each alignment
group of sub-expressions that can be horizontally shifted as a
unit to effect the alignment. Each alignment group must contain one
alignment point. It is also necessary to specify which expressions in
the column have no alignment groups at all, but are affected only by
the ordinary column alignment for that column of the table, i.e. by
the columnalign attribute, described elsewhere.
The alignment groups start at the locations of invisible
maligngroup elements, which are rendered with
zero width when they occur outside of an alignment scope, but within
an alignment scope are rendered with just enough horizontal space to
cause the desired alignment of the alignment group that follows
them. A simple algorithm by which a MathML application can achieve this is given
later. In the example above, each equation would have one
maligngroup element before each coefficient,
variable, and operator on the left-hand side, one before the
= sign, and one before the constant on the right-hand
side.
In general, a table cell containing n
maligngroup elements contains n
alignment groups, with the ith group consisting of the
elements entirely after the ith
maligngroup element and before the
(i+1)-th; no element within the table cell's content
should occur entirely before its first
maligngroup element.
Note that the division into alignment groups does not
necessarily fit the nested expression structure of the MathML
expression containing the groups - that is, it is permissible for one
alignment group to consist of the end of one
mrow, all of another one, and the beginning of a
third one, for example. This can be seen in the MathML markup for the
present example, given at the end of this section.
The nested expression structure formed by mrows
and other layout schemata should reflect the mathematical structure of the
expression, not the alignment-group structure, to make possible optimal
renderings and better automatic interpretations; see the discussion of
proper grouping in section Section 3.3.1 [Horizontally Group Sub-Expressions
(mrow)]. Insertion of
alignment elements (or other space-like elements) should not alter the
correspondence between the structure of a MathML expression and the
structure of the mathematical expression it represents.
Although alignment groups need to coincide with the nested
expression structure of layout schemata, there are nonetheless
restrictions on where an maligngroup element is
allowed within a table cell. The maligngroup
element may only be contained within elements of the following types
(which are themselves contained in the table cell):
mrow element, including an inferred
mrow such as the one formed by a multi-argument
mtd element;
mstyle element;
mphantom element;
mfenced element;
maction element, though only its
selected sub-expression is checked;
semantics element.
These restrictions are intended to ensure that alignment can be unambiguously specified, while avoiding complexities involving things like overscripts, radical signs and fraction bars. They also ensure that a simple algorithm suffices to accomplish the desired alignment.
Note that some positions for an maligngroup
element, although legal, are not useful, such as for an
maligngroup element to be an argument of an
mfenced element. When inserting an
maligngroup element before a given element in
pre-existing MathML, it will often be necessary, and always
acceptable, to form a new mrow element to contain
just the maligngroup element and the element it
is inserted before. In general, this will be necessary except when the
maligngroup element is inserted directly into an
mrow or into an element that can form an
inferred mrow from its contents. See the warning
about the legal grouping of `space-like elements' in
Section 3.2.7 [Space (mspace)].
For the table cells that are divided into alignment groups, every
element in their content must be part of exactly one alignment group,
except the elements from the above list that contain
maligngroup elements inside them, and the
maligngroup elements themselves. This means
that, within any table cell containing alignment groups, the first
complete element must be an maligngroup element,
though this may be preceded by the start tags of other elements.
This requirement removes a potential confusion about how to align
elements before the first maligngroup element,
and makes it easy to identify table cells that are left out of their
column's alignment process entirely.
Note that it is not required that the table cells in a column that are divided into alignment groups each contain the same number of groups. If they don't, zero-width alignment groups are effectively added on the right side of each table cell that has fewer groups than other table cells in the same column.
Expressions in a column that are to have no alignment groups
should contain no maligngroup
elements. Expressions with no alignment groups are aligned using only
the columnalign attribute that applies to the table
column as a whole, and are not affected by the groupalign
attribute described below. If such an expression is wider than the
column width needed for the table cells containing alignment groups,
all the table cells containing alignment groups will be shifted as a
unit within the column as described by the columnalign
attribute for that column. For example, a column heading with no
internal alignment could be added to the column of two equations given
above by preceding them with another table row containing an
mtext element for the heading, and using the
default columnalign="center" for the table, to
produce:
equations with aligned variables
8.44x + 55 y = 0
3.1 x - 0.7y = -1.1
or, with a shorter heading,
some equations 8.44x + 55 y = 0 3.1 x - 0.7y = -1.1
malignmark
Each alignment group's alignment point can either be specified by
an malignmark element anywhere within the
alignment group (except within another alignment scope wholly
contained inside it), or it is determined automatically from the
groupalign attribute. The groupalign
attribute can be specified on the group's preceding
maligngroup element or on its surrounding
mtd, mtr, or
mtable elements. In typical cases, using the
groupalign attribute is sufficient to describe the
desired alignment points, so no malignmark
elements need to be provided.
The malignmark element indicates that the
alignment point should occur on the right edge of the preceding
element, or the left edge of the following element or character,
depending on the edge attribute of
malignmark. Note that it may be necessary to
introduce an mrow to group an
malignmark element with a neighboring element,
in order not to alter the argument count of the containing
element. (See the warning about the legal grouping of `space-like
elements' in Section 3.2.7 [Space (mspace)]).
When an malignmark element is provided within an
alignment group, it can occur in an arbitrarily deeply nested element
within the group, as long as it is not within a nested alignment scope. It
is not subject to the same restrictions on location as maligngroup elements. However, its immediate
surroundings need to be such that the element to its immediate right or
left (depending on its edge attribute) can be
unambiguously identified. If no such element is present, renderers should
behave as if a zero-width element had been inserted there.
For the purposes of alignment, an element X is considered to be to the
immediate left of an element Y, and Y to the immediate right of X, whenever
X and Y are successive arguments of one (possibly inferred) mrow element, with X coming before Y. In the case of
mfenced elements, MathML applications should evaluate this
relation as if the mfenced element had been
replaced by the equivalent expanded form involving mrow. Similarly, an maction
element should be treated as if it were replaced by its currently selected
sub-expression. In all other cases, no relation of `to the immediate
left or right' is defined for two elements X and Y. However, in the
case of content elements interspersed in presentation markup, MathML applications
should attempt to evaluate this relation in a sensible way. For example, if
a renderer maintains an internal presentation structure for rendering
content elements, the relation could be evaluated with respect to
that. (See Chapter 4 [Content Markup] and Chapter 5 [Combining Presentation and Content Markup] for further
details about mixing presentation and content markup.)
Unlike all other elements in MathML,
malignmark elements are allowed to occur within
the content of token elements, such as mn,
mi, or mtext. When this
occurs, the character immediately before or after the
malignmark element will carry the alignment
point; in all other cases, the element to its immediate left or right
will carry the alignment point. The rationale for this is that it is
sometimes desirable to align on the edges of specific characters
within multi-character token elements.
If there is more than one malignmark element
in an alignment group, all but the first one will be ignored. MathML
applications may wish to provide a mode in which they will warn about
this situation, but it is not an error, and should trigger no warnings
by default. (Rationale: it would be inconvenient to have to remove all
unnecessary malignmark elements from
automatically generated data, in certain cases, such as when they are
used to specify alignment on `decimal points' other than the '.'
character.)
In addition to the attributes listed below, the malignmark element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| edge | left | right | left |
malignmark has one attribute,
edge, which specifies whether the alignment point will be
found on the left or right edge of some element or character. The
precise location meant by `left edge' or `right edge' is discussed
below. If edge="right", the alignment point is the right
edge of the element or character to the immediate left of the
malignmark element. If edge="left",
the alignment point is the left edge of the element or character to
the immediate right of the malignmark
element. Note that the attribute refers to the choice of edge rather
than to the direction in which to look for the element whose edge will
be used.
For malignmark elements that occur within
the content of MathML token elements, the preceding or following
character in the token element's content is used; if there is no such
character, a zero-width character is effectively inserted for the
purpose of carrying the alignment point on its edge. For all other
malignmark elements, the preceding or following
element is used; if there is no such element, a zero-width element is
effectively inserted to carry the alignment point.
The precise definition of the `left edge' or `right edge' of a character or glyph (e.g. whether it should coincide with an edge of the character's bounding box) is not specified by MathML, but is at the discretion of the renderer; the renderer is allowed to let the edge position depend on the character's context as well as on the character itself.
For proper alignment of columns of numbers (using groupalign values of left, right, or decimalpoint), it is
likely to be desirable for the effective width (i.e. the distance between
the left and right edges) of decimal digits to be constant, even if their
bounding box widths are not constant (e.g. if `1' is narrower
than other digits). For other characters, such as letters and operators, it
may be desirable for the aligned edges to coincide with the bounding
box.
The `left edge' of a MathML element or alignment group
refers to the left edge of the leftmost glyph drawn to render the element
or group, except that explicit space represented by mspace or mtext elements
should also count as `glyphs' in this context, as should
glyphs that would be drawn if not for mphantom
elements around them. The `right edge' of an element or
alignment group is defined similarly.
In addition to the attributes listed below, the malignmark element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| groupalign | left | center | right | decimalpoint | inherited |
maligngroup has one attribute,
groupalign, which is used to determine the position of
its group's alignment point when no malignmark
element is present. The following discussion assumes that no
malignmark element is found within a group.
In the example given at the beginning of this section, there is one
column of 2 table cells, with 7 alignment groups in each table cell;
thus there are 7 columns of alignment groups, with 2 groups, one above
the other, in each column. These columns of alignment groups should be
given the 7 groupalign values `decimalpoint left left
decimalpoint left left decimalpoint', in that order. How to specify
this list of values for a table cell or table column as a whole, using
attributes on elements surrounding the
maligngroup element is described later.
If groupalign is `left',
`right', or `center', the alignment point is
defined to be at the group's left edge, at its right edge, or halfway
between these edges, respectively. The meanings of `left edge'
and `right edge' are as discussed above in relation to malignmark.
If groupalign is `decimalpoint',
the alignment point is the right edge of the last character before the
decimal point. The decimal point is the first `.' character
(ASCII 0x2e) in the first mn element found along
the alignment group's baseline. More precisely, the alignment group is
scanned recursively, depth-first, for the first mn
element, descending into all arguments of each element of the types
mrow (including inferred
mrows), mstyle,
mpadded, mphantom,
mfenced, or msqrt,
descending into only the first argument of each `scripting' element
(msub, msup,
msubsup, munder,
mover, munderover,
mmultiscripts) or of each
mroot or semantics element,
descending into only the selected sub-expression of each
maction element, and skipping the content of all
other elements. The first mn so found always
contains the alignment point, which is the right edge of the last
character before the first decimal point in the content of the
mn element. If there is no decimal point in the
mn element, the alignment point is the right edge
of the last character in the content. If the decimal point is the
first character of the mn element's content, the
right edge of a zero-width character inserted before the decimal point
is used. If no mn element is found, the right
edge of the entire alignment group is used (as for
groupalign="right").
In order to permit alignment on decimal points in
cn elements, a MathML application can convert a
content expression into a presentation expression that renders the
same way before searching for decimal points as described above.
If characters other than `.' should be used as
`decimal points' for alignment, they should be preceded by malignmark elements within the mn token's content itself.
For any of the groupalign values, if an explicit
malignmark element is present anywhere within
the group, the position it specifies (described earlier) overrides the
automatic determination of alignment point from the
groupalign value.
groupalign valuesIt is not usually necessary to put a groupalign
attribute on every maligngroup element. Since
this attribute is usually the same for every group in a column of
alignment groups to be aligned, it can be inherited from an attribute
on the mtable that was used to set up the
alignment scope as a whole, or from the mtr or
mtd elements surrounding the alignment group. It
is inherited via an `inheritance path' that proceeds from
mtable through successively contained
mtr, mtd, and
maligngroup elements. There is exactly one
element of each of these kinds in this path from an
mtable to any alignment group inside it. In
general, the value of groupalign will be
inherited by any given alignment group from the innermost element
that surrounds the alignment group and provides an explicit
setting for this attribute.
Note, however, that each mtd element needs, in
general, a list of groupalign values, one for each
maligngroup element inside it, rather than just
a single value. Furthermore, an mtr or
mtable element needs, in general, a list of lists
of groupalign values, since it spans multiple
mtable columns, each potentially acting as an
alignment scope. Such lists of group-alignment values are specified
using the following syntax rules:
group-alignment := left | right | center | decimalpoint
group-alignment-list := group-alignment +
group-alignment-list-list := ( '{' group-alignment-list '}' ) +
As described in Section 2.4.4 [MathML Attribute Values], | separates
alternatives; + represents optional repetition (i.e. 1 or
more copies of what precedes it), with extra values ignored and the
last value repeated if necessary to cover additional table columns or
alignment group columns; '{' and '}'
represent literal braces; and ( and ) are
used for grouping, but do not literally appear in the attribute
value.
The permissible values of the groupalign attribute of the
elements that have this attribute are specified using the above
syntax definitions as follows:
| Element type | groupalign attribute syntax | default value |
|---|---|---|
mtable |
group-alignment-list-list | {left} |
mtr |
group-alignment-list-list | inherited from mtable attribute |
mtd |
group-alignment-list | inherited from within mtr attribute |
maligngroup |
group-alignment | inherited from within mtd attribute |
In the example near the beginning of this section, the group
alignment values could be specified on every mtd
element using groupalign = `decimalpoint left left
decimalpoint left left decimalpoint', or on every
mtr element using groupalign =
`{decimalpoint left left decimalpoint left left decimalpoint}', or
(most conveniently) on the mtable as a whole
using groupalign = `{decimalpoint left left decimalpoint
left left decimalpoint}', which provides a single braced list of
group-alignment values for the single column of expressions to be
aligned.
The above rules are sufficient to explain the MathML representation of the example given near the start of this section. To repeat the example, the desired rendering is:
8.44x + 55 y = 0
3.1 x - 0.7y = -1.1
One way to represent that in MathML is:
<mtable groupalign="decimalpoint left left decimalpoint left left decimalpoint">
<mtr>
<mtd>
<mrow>
<mrow>
<mrow>
<maligngroup/>
<mn> 8.44 </mn>
<mo> ⁢ </mo>
<maligngroup/>
<mi> x </mi>
</mrow>
<maligngroup/>
<mo> + </mo>
<mrow>
<maligngroup/>
<mn> 55 </mn>
<mo> ⁢ </mo>
<maligngroup/>
<mi> y </mi>
</mrow>
</mrow>
<maligngroup/>
<mo> = </mo>
<maligngroup/>
<mn> 0 </mn>
</mrow>
</mtd>
<mtd>
<mrow>
<mrow>
<mrow>
<maligngroup/>
<mn> 3.1 </mn>
<mo> ⁢ </mo>
<maligngroup/>
<mi> x </mi>
</mrow>
<maligngroup/>
<mo> - </mo>
<mrow>
<maligngroup/>
<mn> 0.7 </mn>
<mo> ⁢ </mo>
<maligngroup/>
<mi> y </mi>
</mrow>
</mrow>
<maligngroup/>
<mo> = </mo>
<maligngroup/>
<mrow>
<mo> - </mo>
<mn> 1.1 </mn>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
The alignment elements maligngroup and
malignmark can occur outside of alignment
scopes, where they are ignored. The rationale behind this is that in
situations in which MathML is generated, or copied from another
document, without knowing whether it will be placed inside an
alignment scope, it would be inconvenient for this to be an error.
An mtable element can be given the attribute alignmentscope=false to cause its
columns not to act as alignment scopes. In general, this attribute has the
syntax (true | false) +; if its value is a list of boolean
values, each boolean value applies to one column, with the last value
repeated if necessary to cover additional columns, or with extra values
ignored. Columns that are not alignment scopes are part of the alignment
scope surrounding the mtable element, if there is
one. Use of alignmentscope=false allows nested tables to contain malignmark elements for aligning the inner table in the
surrounding alignment scope.
As discussed above, processing of alignment for content elements is not well-defined, since MathML does not specify how content elements should be rendered. However, many MathML applications are likely to find it convenient to internally convert content elements to presentation elements that render the same way. Thus, as a general rule, even if a renderer does not perform such conversions internally, it is recommended that the alignment elements should be processed as if it did perform them.
A particularly important case for renderers to handle gracefully is the
interaction of alignment elements with the matrix
content element, since this element may or may not be internally converted
to an expression containing an mtable element for
rendering. To partially resolve this ambiguity, it is suggested, but not
required, that if the matrix element is converted
to an expression involving an mtable element, that
the mtable element be given the attribute alignmentscope=false, which will
make the interaction of the matrix element with the
alignment elements no different than that of a generic presentation element
(in particular, it will allow it to contain malignmark elements that operate within the alignment
scopes created by the columns of an mtable that
contains the matrix element in one of its table
cells).
The effect of alignment elements within table cells that have
non-default values of the columnspan or rowspan attributes is not specified, except that such
use of alignment elements is not an error. Future versions of MathML may
specify the behavior of alignment elements in such table cells.
The effect of possible linebreaking of an mtable
element on the alignment elements is not specified.
A simple algorithm by which a MathML application can perform the
alignment specified in this section is given here. Since the alignment
specification is deterministic (except for the definition of the left
and right edges of a character), any correct MathML alignment
algorithm will have the same behavior as this one. Each
mtable column (alignment scope) can be treated
independently; the algorithm given here applies to one
mtable column, and takes into account the
alignment elements, the groupalign attribute described in
this section, and the columnalign attribute described
under mtable (Section 3.5.1 [Table or Matrix
(mtable)]).
First, a rendering is computed for the contents of each table cell
in the column, using zero width for all
maligngroup and malignmark
elements. The final rendering will be identical except for horizontal
shifts applied to each alignment group and/or table cell. The
positions of alignment points specified by any
malignmark elements are noted, and the remaining
alignment points are determined using groupalign
values.
For each alignment group, the horizontal positions of the left edge, alignment point, and right edge are noted, allowing the width of the group on each side of the alignment point (left and right) to be determined. The sum of these two `side-widths', i.e. the sum of the widths to the left and right of the alignment point, will equal the width of the alignment group.
Second, each column of alignment groups, from left to right, is scanned. The ith scan covers the ith alignment group in each table cell containing any alignment groups. Table cells with no alignment groups, or with fewer than i alignment groups, are ignored. Each scan computes two maximums over the alignment groups scanned: the maximum width to the left of the alignment point, and the maximum width to the right of the alignment point, of any alignment group scanned.
The sum of all the maximum widths computed (two for each column of alignment groups) gives one total width, which will be the width of each table cell containing alignment groups. Call the maximum number of alignment groups in one cell n; each such cell's width is divided into 2n adjacent sections, called L(i) and R(i) for i from 1 to n, using the 2n maximum side-widths computed above; for each i, the width of all sections called L(i) is the maximum width of any cell's ith alignment group to the left of its alignment point, and the width of all sections called R(i) is the maximum width of any cell's ith alignment group to the right of its alignment point.
The alignment groups are then positioned in the unique way that places the part of each ith group to the left of its alignment point in a section called L(i), and places the part of each ith group to the right of its alignment point in a section called R(i). This results in the alignment point of each ith group being on the boundary between adjacent sections L(i) and R(i), so that all alignment points of ith groups have the same horizontal position.
The widths of the table cells that contain no alignment groups were computed as part of the initial rendering, and may be different for each cell, and different from the single width used for cells containing alignment groups. The maximum of all the cell widths (for both kinds of cells) gives the width of the table column as a whole.
The position of each cell in the column is determined by the
applicable part of the value of the columnalign attribute
of the innermost surrounding mtable,
mtr, or mtd element that
has an explicit value for it, as described in the sections on those
elements. This may mean that the cells containing alignment groups
will be shifted within their column, in addition to their alignment
groups having been shifted within the cells as described above, but
since each such cell has the same width, it will be shifted the same
amount within the column, thus maintaining the vertical alignment of
the alignment points of the corresponding alignment groups in each
cell.
maction)There are many ways in which it might be desirable to make mathematical content active. Adding a link to a MathML sub-expression is one basic kind of interactivity. See Section 7.1.4 [Mixing and Linking MathML and HTML]. However, many other kinds of interactivity cannot be easily accommodated by generic linking mechanisms. For example, in lengthy mathematical expressions, the ability to `fold' expressions might be provided, i.e. a renderer might allow a reader to toggle between an ellipsis and a much longer expression that it represents.
To provide a mechanism for binding actions to expressions, MathML
provides the maction element. This element accepts any
number of sub-expressions as arguments.
In addition to the attributes listed below, this element permits
id,
xref, class and
style attributes,
as described in Section 2.4.5 [Attributes Shared by all MathML Elements].
| Name | values | default |
|---|---|---|
| actiontype | (described below) | (required attribute, no default value) |
| selection | positive-integer | 1 |
By default, MathML applications that do not recognize the specified
actiontype should render the selected sub-expression as
defined below. If no selected sub-expression exists, it is a MathML
error; the appropriate rendering in that case is as described in
Section 7.2.2 [Handling of Errors].
Since a MathML-compliant application is not required to recognize any
particular actiontypes, an application can be fully MathML
compliant just by implementing the above-described default behavior.
The selection attribute is provided for those
actiontypes that permit someone viewing a document to select one of
several sub-expressions for viewing. Its value should be a positive
integer that indicates one of the sub-expressions of the
maction element, numbered from 1 to the number of
children of the element. When this is the case, the sub-expression so
indicated is defined to be the `selected sub-expression' of the
maction element; otherwise the `selected
sub-expression' does not exist, which is an error. When the
selection attribute is not specified (including for
actiontypes for which it makes no sense), its default value is 1, so
the selected sub-expression will be the first sub-expression.
Furthermore, as described in Chapter 7 [The MathML Interface], if a MathML
application responds to a user command to copy a MathML sub-expression to
the environment's `clipboard', any maction elements present in what is copied should
be given selection attributes that correspond to their selection
state in the MathML rendering at the time of the copy command.
A suggested list of actiontypes and their associated
actions is given below. Keep in mind, however, that this list is
mainly for illustration, and recognized values and behaviors will vary
from application to application.
selection attribute value as described above.
Typical uses would be for exercises in education, ellipses in long
computer algebra output, or to illustrate alternate notations. Note
that the expressions may be of significantly different size, so that
size negotiation with the browser may be desirable. If size
negotiation is not available, scrolling, elision, panning, or some
other method may be necessary to allow full viewing.mtext element for the message in most circumstances.
For non-mtext messages, renderers might provide a
natural language translation of the markup, but this is not
required.mtext element for the message
in most circumstances. For non-mtext messages,
renderers may provide a natural language translation of the markup if
full MathML rendering is not practical, but this is not
required.my:color attribute
changes the color of the characters in the presentation, while the
my:background attribute changes the color of the background
behind the characters.
Overview: Mathematical Markup Language (MathML) Version 2.0
Previous: 2 MathML Fundamentals
Next: 4 Content Markup