1 導入
概要: 数学用マークアップ言語 (MathML) バージョン 2.0 日本語版
次: 2 MathML の基礎
1 導入
1.1 数学とその表記法
1.2 起源と目的
1.2.1 MathML の歴史
1.2.2 HTML の制約
1.2.3 数学のマークアップにおける要請事項
1.2.4 MathML の設計上の目標
1.3 ウェブ上で MathML が果たす役割
1.3.1 階層化された数学ウェブサービス
1.3.2 他のウェブ技術との関連
1.1 数学とその表記
複雑で高度に発達した 2 次元の記号による表記体系の使用は、数学の際だった特徴です。
J.R.Pierceが彼のコミュニケーション理論に関する著書の中で述べたように、数学とその表記法は同一視するべきではありません
[Pierce1961]。
数学的思想と、それを表現するための表記法は、独立して存在しています。
しかしながら、「意味」と「表記」の間の関係は微妙です。
数学において、事象を記述したり解析したりできるということは、思想を表象的な形で表現して扱えるからこそです。
ウェブ上に数学を載せる際に、高度に発達した印刷の表記上の慣例や電子メディアにおける相互接続性の能力を文書から活用できるよう、内容 (つまり、意味) と表記の両方を記録することは非常に困難です。
A distinguishing feature of mathematics is the use of a complex and
highly evolved system of two-dimensional symbolic notations. As
J.R. Pierce has written in his book on communication theory,
mathematics and its notations should not be viewed as one and the same
thing [Pierce1961]. Mathematical ideas exist independently of
the notations that represent them. However, the relation between meaning
and notation is subtle, and part of the power of mathematics to describe
and analyze derives from its ability to represent and manipulate ideas in
symbolic form. The challenge in putting mathematics on the World Wide Web
is to capture both notation and content (that is, meaning) in such a way
that documents can utilize the highly-evolved notational forms of written
and printed mathematics, and the potential for interconnectivity in
electronic media.
数学の表記法は、人々が思考を扱い表現する画期的な方法を発明し続けるにつれ、絶え間なく発達します。
今では常識となった代数学の表記法ですら、それぞれの時代の最先端の数学によって支持されたり廃れてしまったりを繰り返しながら、驚くほど多くの形式を基礎としてました [Cajori1928]。
近代の数学の表記法は「改良の世紀」の産物であり、そして高品質な活字を行うために、表記法の慣行は複雑の極みとなりました。
たとえば、数字の代わりに表すための記号、つまり変数は、文章用の斜体文字とは微妙に異なった特別な斜体の活字を用いるのが、現在の一般的な方法です。
+−×÷のような演算記号の字間は、演算子の優先順位の慣行を反映し、文章のそれとは微妙に異なっています。
上付文字と下付文字の位置関係、括弧の大きさの選び方の法則から、数学の下位分野に特化された表記法の慣例に至るまで、数学用の活字の慣行だけのために何冊もの本が書かれてきました。
(たとえば [Chaundy1954]、[Swanson1979]、[Swanson1999]、[Higham1993]、また TEX については [Knuth1986]や[Spivak1986]など)
Mathematical notations are constantly evolving as people continue
to make innovations in ways of approaching and expressing ideas. Even
the commonplace notations of arithmetic have gone through an amazing
variety of styles, including many defunct ones advocated by leading
mathematical figures of their day [Cajori1928]. Modern
mathematical notation is the product of centuries of refinement, and
the notational conventions for high-quality typesetting are quite
complicated. For example, variables and letters which stand for
numbers are usually typeset today in a special mathematical italic
font subtly distinct from the usual text italic. Spacing around
symbols for operations such as +, -, × and / is slightly
different from that of text, to reflect conventions about operator
precedence. Entire books have been devoted to the conventions of
mathematical typesetting, from the alignment of superscripts and
subscripts, to rules for choosing parenthesis sizes, and on to
specialized notational practices for subfields of mathematics (for
instance, [Chaundy1954], [Swanson1979],[Swanson1999], [Higham1993], or in the TEX literature [Knuth1986] and [Spivak1986]).
数学や一般の印刷物における表記上の慣行は、視線を導き、印刷された表現を読解しやすくします。
しかし、普段私たちは当然のように考えていますが、私たちは段落や大文字小文字、書体や書式、あるいはこの文書で用いられているような節ごとに小数のような番号付けをする工夫 (G.Peano による発明。おそらく彼は自然数の公理についての方がよく知られているでしょうが) まで、何百という慣行に依存しているのです。
そうした記号法の慣行は、画面上で読む際の困難に妥協を必要とする電子メディアにおいて、より重要となるのです。
Notational conventions in mathematics, and in printed text in general,
guide the eye and make printed expressions much easier to read and
understand. Though we usually take them for granted, we rely on
hundreds of conventions such as paragraphs, capital letters, font
families and cases, and even the device of decimal-like numbering of
sections such as we are using in this document (an invention due to
G. Peano, who is probably better known for his axioms for the
natural numbers). Such notational conventions are perhaps even more important
for electronic media, where one must contend with the difficulties of
on-screen reading.
しかしながら、数学をウェブに載せると言うことは、単に伝統的な数学の記号法をウェブブラウザーの中で表示させる方法を見つければよいと言うわけではありません。
ウェブは、知識の貯蔵に対する潜在的なメタファーの根本的変化、つまり 相互接続性 が中心的な役割を果たす変化を象徴しています。
機械的な処理・検索・番号付け、そして他の数学アプリケーションや場面での再利用が円滑に行えるように数学を伝達する手段を探し出すことが、いよいよ重要になってきています。
このコミュニケーション技術の進歩によって、数学の見解やお互いの理解を描画・符号化し、そして最終的には相互に通信する能力を引き延ばせるかもしれません。
私たちは、MathML がウェブにおける数学の発達の重要なステップであると信じています。
However, there is more to putting mathematics on the Web
than merely finding ways of displaying traditional
mathematical notation in a Web browser. The Web represents a
fundamental change in the underlying metaphor for knowledge
storage, a change in which interconnectivity
plays a central role. It is becoming increasingly important to
find ways of communicating mathematics which facilitate
automatic processing, searching and indexing, and reuse in
other mathematical applications and contexts. With this
advance in communication technology, there is an opportunity
to expand our ability to represent, encode, and ultimately to
communicate our mathematical insights and understanding with
each other. We believe that MathML is an important step in
developing mathematics on the Web.
1.2 起源と目標
1.2.1 MathML の歴史
コンピューター処理や電子通信のために数学を符号化するという問題は、ウェブよりはるかに古い歴史を持っています。
ウェブ以前に科学者の間で慣例となっていた方法は、ASCII 文字セットを用いて特定の書式で符号化し、それらをお互いに電子メールで送りあうことでした。
1992 年にウェブが広範に利用されるようになる直前には、TEX に代表されるいくつかの数学用のマークアップの方法が確立されていました
[Knuth 1986]、[Poppelier1992]。
The problem of encoding mathematics for computer processing
or electronic communication is much older than the Web. The
common practice among scientists before the Web was to write
papers in some encoded form based on the ASCII character set,
and e-mail them to each other. Several markup methods for
mathematics, in particular TEX [Knuth1986],
were already in wide use in 1992 just before the Web rose to
prominence, [Poppelier1992].
ウェブは発端当初から、各地に散らばった人々が情報を入手できる非常に効果的な方法を証明してきました。
しかし、ワールド・ワイド・ウェブは元々、科学者によって科学者のために生み出され、導入されたものであったにも関わらず、HTML の中に数学的な表現を埋め込む能力は非常に限定されていました。
現時点では、ウェブ上の数学のほとんどは、読みづらくて作成も楽ではない、科学的な表記を埋め込んだ GIF や JPEG のような画像と文字を組み合わせたものであったり、全体の文書を PDF にしているか、のどちらかです。
Since its inception, the Web has demonstrated itself to be
a very effective method of making information available to
widely separated groups of individuals. However, even though
the World Wide Web was initially conceived and implemented by
scientists for scientists, the possibilities for including
mathematical expressions in HTML has been very limited. At
present, most mathematics on the Web consists of text with
images of scientific notation (in GIF or JPEG format), which are difficult to read and
to author, or of entire documents in PDF form.
World Wide Web Consortium (W3C) は、科学的な情報伝達に対する対応不足を、深刻な問題であると認識しています。
Dave Raggett は、1994 年の HTML 3.0 の草案の中に HTML Math の提案を既に包括していました。
1995 年 4 月にドイツ・ダルムシュタットの WWW 協議会で、数学のマークアップに関する公開討論会が開かれました。
同年 11 月には、Wolfram Research 社の代表が W3C チームに対し、HTMLで数学を表現するための提議書を提出しました。
1996 年の 5 月、合衆国シャンペーン・アーバナでの Digital Library Initiative の会議は、多くの関連団体を呼び集めるという重要な役割を果たしました。
その会議の後、HTML 数学論説審議会が設立されました。
この団体は成長し、その後 1997 年 3 月に W3C 数学ワークグループとして再編されました。
W3C 数学ワークグループは、1998 年 7 月に 2 度目の招集がなされ、その後 2000 年末までの期間続きました。
The World Wide Web Consortium (W3C) recognized that lack of
support for scientific communication was a serious
problem. Dave Raggett included a proposal for HTML Math in the
HTML 3.0 working draft in 1994. A panel discussion on
mathematical markup was held at the WWW Conference in
Darmstadt in April 1995. In November 1995, representatives
from Wolfram Research presented a proposal for doing mathematics in
HTML to the W3C team. In May 1996, the Digital Library
Initiative meeting in Champaign-Urbana played an important
role in bringing together many interested parties. Following
the meeting, an HTML Math Editorial Review Board was
formed. In the intervening years, this group has grown, and
was formally reconstituted as the first W3C Math Working Group
in March 1997. The second W3C Math Working Group was
chartered in July 1998 with a term which was later extended to run
to the end of the year 2000.
MathML の提議書は、非常に多様な団体の関心や専門知識を反映しています。
MathML の開発に携わった多くの貢献者たちは、表彰に値するものです。ここでその一部をご紹介いたします。
T.V.Raman 氏は、アクセシビリティの問題、特に視覚的障害者に対する問題について貢献しました。
Wolfram Research 社の Neil Soiffer 氏と Bruce Smith 氏は、その経験を生かして、プレゼンテーション要素の設計に多大な影響を及ぼした Mathematica 3.0 の仕様と互換性を保って表現を表記する問題に取り組みました。
Design Science 社の Paul Topping 氏もまた、その数学の書式や編集における専門知識で貢献しました。
MathML は、SGML での数学の符号化の問題に取り組んだ多くのワークグループのメンバーや、Elsevier Science 社の Nico Poppelier 氏や INRIA の Ste'phane Dalmas 氏、Waterloo Maple 社の Sophia Antipolis 氏と Stan Devitt 氏、IBM 社の Angel Diaz 氏と Tobert S. Sutor 氏、そして Western Ontario 大学の Stephen M. Watt 氏といった、多くの人々の参加の恩恵を受けました。
MathML は semantic な数学の DTD の一部に、特に ISO 12083 のワークグループの OpenMath プロジェクトや、Stilo Technologies 社の研究の影響を受けています。
米国数学学会は、MathML の発展に鍵となる役割を果たしました。
数ある中でもこの学会からは、 Ron Whitney 氏 (1996 年 5 月から 1997 年 3 月までグループを指揮した) と Patrik Ion 氏 (1997年 3 月から1998 年 7 月までは Geometry Center の Robert Miner 氏と、その後は IBM の Angel Diaz 氏とともにグループの代表を務めてきた) の二人の代表が選出されました。
The MathML proposal reflects the interests and expertise of
a very diverse group. Many contributions to the development of
MathML deserve special mention, some of which we touch on
here. One such contribution concerns the question of
accessibility, especially for the visually handicapped.
T. V. Raman is particularly notable in this
regard. Neil Soiffer and Bruce Smith from Wolfram Research
shared their experience with the problems of representing
mathematics in connection with the design of Mathematica 3.0;
this expertise was an important influence in the design of the
presentation elements. Paul Topping from Design Science also
contributed his expertise in mathematical formatting and
editing. MathML has benefited from the participation of a
number of working group members involved in other mathematical
encoding efforts in the SGML and
computer-algebra communities, including Stephen Buswell from
Stilo Technologies, Nico Poppelier at first with Elsevier
Science, Stéphane Dalmas from INRIA (Sophia Antipolis),
Stan Devitt at first with Waterloo Maple, Angel Diaz and
Robert S. Sutor from IBM, and Stephen M. Watt from
the University of Western Ontario. In particular, MathML has
been influenced by the OpenMath project, the work of the ISO
12083 working group, and Stilo Technologies' work on a
`semantic' mathematics DTD fragment. The American
Mathematical Society has played a key role in the development
of MathML. Among other things, it has provided two working
group chairs: Ron Whitney led the group from May 1996 to March
1997, and Patrick Ion, who has co-chaired the group with
Robert Miner from The Geometry Center from March 1997 to
June 1998, and since July 1998 with Angel Diaz of IBM.
1.2.2 HTML の限界
科学的な情報交換を電子的に行う効果的な手段が強く求められています。
研究者、科学者、技師、教師、学生、技術者は、ますます遠隔地で働くようになり、電子通信に依存するようになっています。
同時に、現在ウェブで科学的な表記を伝達する手段として主に用いられている画像主体の方法は、原始的で不適当なものです。
というのも、文書の質は低く、制作は困難で、しかも画像に含まれる数学的な情報は、検索や番号付け、あるいは他のアプリケーションでの再利用ができないからです。
The demand for effective means of electronic scientific
communication remains high. Ever increasingly, researchers,
scientists, engineers, educators, students and technicians
find themselves working at dispersed locations and relying on
electronic communication. At the same time, the image-based
methods that are currently the predominant means of
transmitting scientific notation over the Web are primitive
and inadequate. Document quality is poor, authoring is
difficult, and mathematical information contained in images is
not available for searching, indexing, or reuse in other
applications.
HTML で数学的な情報を交換する際の明らかな問題は、大きく 2 つに分類できます。
The most obvious problems with HTML for mathematical
communication are of two types.
表示上の問題。
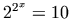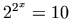 という数式について考えてみましょう。
この数式は、制作された環境 (周囲の文字が14ポイント) に合う大きさで作成されています。
当然、他の環境、つまり他のフォントの大きさでは、この数式は小さすぎたり大きすぎたりします。
次に気がつくのは、この数式の画像は白い背景に対して作られたということです。
従って、読み手やブラウザーがページの背景色を他の色に変えてしまうと、画像のアンチエイリアスの部分は白い「後光 (halo) 」になってしまいます。
という数式について考えてみましょう。
この数式は、制作された環境 (周囲の文字が14ポイント) に合う大きさで作成されています。
当然、他の環境、つまり他のフォントの大きさでは、この数式は小さすぎたり大きすぎたりします。
次に気がつくのは、この数式の画像は白い背景に対して作られたということです。
従って、読み手やブラウザーがページの背景色を他の色に変えてしまうと、画像のアンチエイリアスの部分は白い「後光 (halo) 」になってしまいます。
Display Problems. Consider the equation
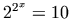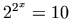 . This equation
is sized to match the surrounding line in 14pt type on the
system where it was authored. Of course, on other systems, or
for other font sizes, the equation is too small or too
large. A second point to observe is that the equation image
was generated against a white background. Thus, if a reader or
browser resets the page background to another color, the
anti-aliasing in the image results in white
`halos'.
. This equation
is sized to match the surrounding line in 14pt type on the
system where it was authored. Of course, on other systems, or
for other font sizes, the equation is too small or too
large. A second point to observe is that the equation image
was generated against a white background. Thus, if a reader or
browser resets the page background to another color, the
anti-aliasing in the image results in white
`halos'.
次に、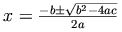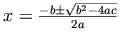 という数式を考えてみましょう。
これは周囲の文字の最上部よりも上に、水平の中心軸がある例です。
この数式には、ディセンダー (訳注: g や j などの下に出た部分) があるため、数式の基準線が画像の最下部から 1/3 ほどの所にあります。
この画像は、
という数式を考えてみましょう。
これは周囲の文字の最上部よりも上に、水平の中心軸がある例です。
この数式には、ディセンダー (訳注: g や j などの下に出た部分) があるため、数式の基準線が画像の最下部から 1/3 ほどの所にあります。
この画像は、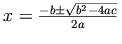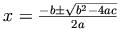 と配置することもできます。
こうすることにより、画像の中心線と数式の基準線が一致しますが、しかし行間隔の問題が発生し、結局数式が読みにくくなってしまいます。
さらに、画像の中心位置はブラウザーが異なれば処理のされ方も微妙に違うため、異なるクライアントに対して適切な位置関係を保証することが不可能になります。
と配置することもできます。
こうすることにより、画像の中心線と数式の基準線が一致しますが、しかし行間隔の問題が発生し、結局数式が読みにくくなってしまいます。
さらに、画像の中心位置はブラウザーが異なれば処理のされ方も微妙に違うため、異なるクライアントに対して適切な位置関係を保証することが不可能になります。
Next, consider the equation 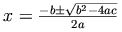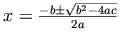 , which is an example
with the equation's horizontal alignment axis above the tops
of the lower-case letters in the surrounding text.
This equation has a descender which places the baseline for
the equation at a point about a third of the way from the
bottom of the image. One can pad the image like this:
, which is an example
with the equation's horizontal alignment axis above the tops
of the lower-case letters in the surrounding text.
This equation has a descender which places the baseline for
the equation at a point about a third of the way from the
bottom of the image. One can pad the image like this:
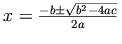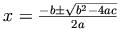 ,
so that the centerline of the image and the baseline of the
equation coincide, but this causes problems with the
inter-line spacing, resulting in the equation becoming
difficult to read. Moreover, center alignment of images is
handled in slightly different ways by different browsers,
making it impossible to guarantee proper alignment for
different clients.
,
so that the centerline of the image and the baseline of the
equation coincide, but this causes problems with the
inter-line spacing, resulting in the equation becoming
difficult to read. Moreover, center alignment of images is
handled in slightly different ways by different browsers,
making it impossible to guarantee proper alignment for
different clients.
画像主体の数式は、ブラウザーのウインドウの中では一般的に周囲の文字に比べて見づらくて読みにくく、そして理解しづらいものです。
しかも、こうした問題は文書が印刷されるといっそうひどくなります。数式の画像の解像度は 70dpi 程度なのに、周囲の文字は普通 300dpi や 600dpi 以上で印刷されます。
こうした画質の不一致は、多くの人にとって受け入れがたいものと判断されます。
Image-based equations are generally harder to see, read and
comprehend than the surrounding text in the browser
window. Moreover, these problems become worse when the
document is printed. The resolution of the equations as images
will be around 70 dots per inch, while the surrounding text
will typically be 300, 600 or more dots per inch. The
disparity in quality is judged to be unacceptable by most
people.
符号化の問題。
このページ内から数式の一部、たとえば上記の数式から「=10」の部分を検索することを考えてみましょう。
同じように、他のアプリケーションに数式をカット & ペーストすることを考えてみましょう。
もちろん、求められているのはその意味もカット & ペーストすることです。
画像主体の方法では、こうした一般的なニーズのいずれも適切に処理するできません。
文書のソース中における alt 文字列の使用も役には立ちますが、ウェブではせっかく情報が高度に相互作用しているのですから、ブラウザーと数学表記の間にも、より洗練されたインターフェースがほしいものです。
Encoding Problems. Consider trying to search
this document for part of an equation, for example, the
`=10' from the first equation above. In a similar
vein, consider trying to cut and paste an equation into
another application; even more demanding is to cut and paste a
sub-expression. Using image-based methods, neither of these
common needs can be adequately addressed. Although the use of
the alt attribute in the document source can help, it is clear
that highly interactive Web documents must provide a more
sophisticated interface between browsers and mathematical
notation.
数学を画像として符号化する際のもう一つの問題は、より広い帯域幅を必要とすることです。
マークアップによって数式を記述すれば、一般的に画像に比べてより小さく圧縮された状態になります。
加えて、マークアップ主体の符号化を利用すれば、より多くのレンダリング処理がクライアント側の機械へと移されます。
Another problem with encoding mathematics as images is that
it requires more bandwidth. Markup describing an equation is
typically smaller and more compressible than an image of the
equation. In addition, by using markup-based encoding, more
of the rendering process is moved to the client machine.
1.2.3 数学のマークアップにおける要請事項
HTML 文書中に画像として数学の表記を埋め込むことに関する問題の中には、ブラウザーの画像処理能力の改善によって解決できるものもあります。
しかし、たとえ画像処理が改善されても、数式中の情報を他のアプリケーションで利用できるようにするという問題が残っています。
つまり、将来のことを考えるのであれば、単に画像主体の方法を改良するだけでは十分ではないのです。
数学の素材を完全にウェブ文書に統合させるためには、数学の表記法と内容のマークアップによる符号化が必要なのです。
Some display problems associated with including
mathematical notation in HTML documents as images could be
addressed by improving image handling by browsers. However,
even if image handling were improved, the problem of making
the information contained in mathematical expressions
available to other applications would remain. Therefore, in
planning for the future, it is not sufficient merely to
upgrade image-based methods. To integrate mathematical
material fully into Web documents, a markup-based encoding of
mathematical notation and content is required.
どんなマークアップ言語であれ、設計の際にその潜在的な利用者のニーズを注意深く考慮することが大切です。
MathML の場合には、潜在的な利用者のニーズは教育から研究、商業に至るまで広範囲にわたります。
In designing any markup language, it is essential to
consider carefully the needs of its potential users. In the
case of MathML, the needs of potential users cover a broad
spectrum, from education to research, and on to commerce.
教育界は、科学的な教育課程の素材をウェブ上におけることを求めている、大きく重要な団体です。
同時に、教育者達は限られた時間と設備しか持っておらず、その上技術的なウェブ文書を制作することが困難であることが少なくありません。
学生と教師は、直感的で憶えやすく、安価なツールを使用して、数学的なコンテンツを素早く簡単に作成できることを必要とします。
The education community is a large and important group that
must be able to put scientific curriculum materials on the
Web. At the same time, educators often have limited time and
equipment, and are severely hampered by the difficulty of
authoring technical Web documents. Students and teachers need
to be able to create mathematical content quickly and easily,
using intuitive, easy-to-learn, low-cost tools.
電子教材は、教育において重要になりそうな、もう一つのウェブの使い方です。
経営コンサルタントの Peter Drucker 氏は、大きなキャンパスでの高等教育が終わり、ウェブを通じてその供給が行われるようになる、と予想しています。
電子教材はインタラクティブであり、教材と科学的なソフトウェアやグラフィックとの間で相互通信できなければなりません。
Electronic textbooks are another way of using the Web which will
potentially be very important in education. Management consultant
Peter Drucker has prophesied the end of big-campus residential higher
education and its distribution over the Web. Electronic textbooks
will need to be interactive, allowing intercommunication between the
text and scientific software and graphics.
学術研究機関や商用研究機関は、濃密な科学的コンテンツを大量に生産しています。研究出版物はデータベースにどんどん蓄積されています。
その良い例が、Los Alamos 国立研究所の physics and mathematics preprint server and archiveです。
特に、物理学や数学では、分野によって学術機関誌の価格が納得できないペースで上昇しているのが実際です。
加えて、Mathematical Reviews や Zentralblatt für Mathematik のような研究情報のデータベースがウェブ上で数学に関する数百万というデータを提供しています。
The academic and commercial research communities generate large
volume of dense scientific material. Increasingly, research
publications are being stored in databases, such as the highly
successful physics and mathematics
preprint server and archive at Los Alamos National
Laboratory. This is especially true in some areas of physics and
mathematics where academic journal prices have been increasing at an
unsustainable rate. In addition, databases of information on
mathematical research, such as Mathematical Reviews and
Zentralblatt für
Mathematik, offer millions of records on the Web containing
mathematics.
研究機関を取り込むためには、数学のマークアップの設計は、膨大な文書の収集物の保守や操作を簡単にしなければならず、自動的な検索と索引付けが重要になります。
特に、TEX 文書のような遺産データが大量に収集されているので、研究機関にとっては既存のフォーマットと新しいフォーマットの間での変換能力も重要です。
最後に、学術研究機関にとっては、アーカイブする目的のために、情報保守の能力が死活問題となります。
To accommodate the research community, a design for
mathematical markup must facilitate the maintenance and
operation of large document collections, for which automatic
searching and indexing are important. Because of the large
collection of legacy documents containing mathematics, especially in
TEX, the ability to convert between existing formats and any
new one is also very important to the research community.
Finally, the ability to maintain information for archival
purposes is vital to academic research.
企業や高等研究機関の科学者や技師たちもまた、共同研究したり、実験やコンピュータシミュレーションの結果を記録したり、計算を確認したりするために、仕事で技術的な文書を使用します。
そのような使用のために、ウェブ上での数学は、一般的に入手可能なツールを用いて簡単に読んだり処理したり制作できたりする、といった情報共有の標準的な方法を提供しなければなりません。
Corporate and academic scientists and engineers also use
technical documents in their work to collaborate, to record
results of experiments and computer simulations, and to verify
calculations. For such uses, mathematics on the Web must
provide a standard way of sharing information that can be
easily read, processed and generated using commonly available,
easy-to-use tools.
設計上のもう一つの必要条件は、発話装置や点字のような他のメディアで数学の素材を表現できることです。これは視覚障害者にとっては非常に重要です。
Another general design requirement is the ability to render
mathematical material in other media such as speech or
braille, which is extremely important for the visually
impaired.
商業的な出版者も同様に、印刷書籍の電子版やインタラクティブな教材から学術的な刊行誌に至るまですべての水準で、ウェブ上の数学と関わりがあります。
出版社が求めるのは、高画質な出力が可能で、商用で拡大に耐えうるほどに頑強で、そしてできれば従来の SGML 主体の発行システムと互換性を保ってウェブ上に数学を掲載する方法です。
Commercial publishers are also involved with mathematics on
the Web at all levels from electronic versions of print books
to interactive textbooks and academic journals. Publishers
require a method of putting mathematics on the Web that is
capable of high-quality output, robust enough for large-scale
commercial use, and preferably compatible with their previous,
often SGML-based, production systems.
1.2.4 MathML の設計上の目標
科学的な組織の多様なニーズを満たすために、MathML は以下に掲げる項目を最終目標として設計されています。
In order to meet the diverse needs of the scientific
community, MathML has been designed with the following
ultimate goals in mind.
MathML は、こうあるべきです :
MathML should:
-
数学の素材をすべての水準で、教育や科学的情報通信に適するよう符号化するべき
Encode mathematical material suitable for teaching
and scientific communication at all levels.
-
数学上の表記法と内容の両方を符号化するべき
Encode both mathematical notation and mathematical meaning.
-
表示上も意味上も、他の数学のフォーマットとの間で簡単に変換できるべき。出力されるフォーマットには
Facilitate conversion to and from other mathematical
formats, both presentational and semantic. Output formats should include:
- グラフィカルな表示装置
graphical displays
- 発声合成音声装置
speech synthesizers
- 数式処理システムの入力装置
input for computer algebra systems
- TEX のような他の数学レイアウト言語
other mathematics typesetting languages, such as TEX
- VT100 エミュレーターのような、プレーンテキストの表示装置
plain text displays, e.g. VT100 emulators
- 点字を含めた、印刷メディア
print media, including braille
を含むべき。
なお、他の表記システムやメディアとの間での変換によって、その処理の過程で情報の欠落を伴う可能性があることも考えられます。
It is recognized that conversion to and from other notational
systems or media may entail loss of information in the process.
- 特定のレンダラーやアプリケーションに要求される情報を出力できるべき
Allow the passing of information intended for
specific renderers and applications.
- 長ったらしい数式を効率的に閲覧できるべき
Support efficient browsing of lengthy expressions.
- 拡張性を残しているべき
Provide for extensibility.
- テンプレートや他の数学編集技術によく適合できるべき
Be well suited to template and other mathematics editing techniques.
- 人間が判読でき、そしてソフトウェアによる生成と処理が単純であるべき
Be human legible, and simple for software to generate and process.
いかに MathML がマークアップ言語としてその目標を上々に達成したとしても、MathML は十分に実装されなければ便利でないということは明らかです。
この目的のために、W3C 数学ワークグループは、追加の実装についての目標を簡単な一覧で別に用意しています。これらの目標は、MathML の描画ソフトウェアや処理ソフトウェアが提供しようとするであろう最低限の機能性について簡単に記述することを企図しています。
No matter how successfully MathML may achieve its goals as
a markup language, it is clear that MathML will only be useful
if it is implemented well. To this end, the W3C Math Working
Group has identified a short list of additional implementation
goals. These goals attempt to describe concisely the minimal
functionality MathML rendering and processing software should
try to provide.
- HTML (と XHTML) のページ中の MathML の数式は、一般に普及しているウェブブラウザーで読者や制作者の見方の好みに従って適切に描画されるべきで、プラットフォームの能力最大の高画質に描画されるべきです
MathML expressions in HTML (and XHTML) pages should render
properly in popular Web browsers, in accordance with reader and author
viewing preferences, and at the highest quality possible given the
capabilities of the platform.
- MathML の数式を含む HTML (と XHTML) 文書は、適切に、しかもプリンターの高画質な解像度で印刷されるべきです
HTML (and XHTML) documents containing MathML expressions should
print properly and at high-quality printer resolutions.
- ウェブページ中の MathML の数式は、マウスの動作のようなユーザーの挙動に反応できるべきで、そしてブラウザーを通じて他のアプリケーションと情報交換することを可能にするべきです。
MathML expressions in Web pages should be able to react to
user gestures, such those as with a mouse, and to coordinate
communication with other applications through the
browser.
- 数式エディターや変換プログラムは、MathML を含むウェブページの制作を容易にするよう開発されるべきです。
Mathematical expression editors and converters should be developed
to facilitate the creation of Web pages containing MathML
expressions.
こうした目標は、MathML レンダラーとして Java アプレットやプラグイン、ActiveX コントロールなどの埋め込み要素を用いて近いうちに実現されようとしています。
しかしながら、こうした目標が最終的にどこまで辿り着くかは、ブラウザーのベンダーや他のソフトウェア開発者の協力と支持次第なのです。W3C 数学ワークグループは、現在まで文書オブジェクトモデル (Document Object Model; DOM) ワークグループや eXtensible Style Language (XSL; 拡張可能なスタイル言語) ワークグループと、科学に携わる人々のニーズが将来的に満たされるように、協力してきました。
この方面について MathML 2.0 が MathML 1.0 勧告 (1998 年 4 月) の頃に比べて相当の進歩を遂げたと考えています。
These goals have begun to be addressed for the near term by
using embedded elements such as Java applets, plug-ins and
ActiveX controls to render MathML. However, the extent to
which these goals are ultimately met depends on the
cooperation and support of browser vendors, and other software
developers. The W3C Math Working Group has continued to work
with the working groups for the Document Object Model (DOM)
and the Extensible Style Language (XSL) to ensure that the
needs of the scientific community will be met in the future,
and feels that MathML 2.0 shows considerable progress in this
area over the situation that obtained at the time of the
MathML 1.0 Recommendation (April 1998).
1.3 ウェブにおける MathML の役割
1.3.1 階層化された数学ウェブサービス
MathML の設計上の目標の達成には、柔軟で拡張性に富み、外部のソフトウェアとの相互作用に適していて、メディアによっては品質の高い描画ができる、ウェブ用に数学の素材を符号化できるシステムが必要です。
こうした作業をこなすのに十分な情報を符号化できるマークアップ言語であれば、必ず複雑になってしまいます。
The design goals of MathML require a system for encoding
mathematical material for the Web which is flexible and
extensible, suitable for interaction with external software,
and capable of producing high-quality rendering in several
media. Any markup language that encodes enough information to
do all these tasks well will of necessity involve some
complexity.
同時に、学生をはじめとする多くの集団にとって、ウェブページに人の手によって簡単に数学を掲載する方法も必要です。
同様に TEX ユーザーにとっては、ウェブページに TEX のようにマークアップ言語を直接書き込めるシステムがあるべきでしょう。一般的には、特定のユーザーグループに対してそのニーズにうまく特化させた入力と出力があれば、よりよいサービスを提供できます。
ウェブで数学の情報伝達をするための理想的なシステムは、専門的な入出力サービスと、情報交換と複数のメディアへの描画のための一般的なサービスの両方を提供するべきなのです。
At the same time, it is important for many groups, such as
students, to have simple ways to include mathematics in Web
pages by hand. Similarly, other groups, such as the TEX
community, would be best served by a system which allowed the
direct entry of markup languages like TEX into Web pages. In
general, specific user groups are better served by specialized
kinds of input and output tailored to their needs. Therefore,
the ideal system for communicating mathematics on the Web
should provide both specialized services for input and output,
and general services for interchange of information and
rendering to multiple media.
実際問題として、ウェブにおける数学は、専門的なニーズと一般的なニーズの両方に対応するべきだという知見により、自然と階層的な構造の着想に辿り着きます。一つ目の層は、符号化された数学のデータを適切に交換、処理、描画できる、強力で一般的なソフトウェアツールから構成されます。
もう一つの層は、特定のユーザーグループを対象とし、簡単に符号化された数学データを作成して特定の読者と共有できるようにする、専門的なソフトウェアツールから構成されます。
In practical terms, the observation that mathematics on the
Web should provide for both specialized and general needs
naturally leads to the idea of a layered architecture. One
layer consists of powerful, general software tools exchanging,
processing and rendering suitably encoded mathematical data. A
second layer consists of specialized software tools, aimed at
specific user groups, which are capable of easily generating
encoded mathematical data that can then be shared with a
particular audience.
MathML は、二層式の構造の中で最下層、つまりより一般的な層に符号化された数学データを提供するように設計されています。
MathML は、系統立てて規則正しく、そして簡単に描画、検索、番号付けするソフトウェアおよび他の数学アプリケーションが処理できるように、複雑な表記と見た目の構造を符号化することを目的としています。
MathML is designed to provide the encoding of mathematical
information for the bottom, more general layer in a two-layer
architecture. It is intended to encode complex notational and
semantic structure in an explicit, regular, and
easy-to-process way for renderers, searching and indexing
software, and other mathematical applications.
結果的に、MathML は制作者によって直接使用することを第一に想定しているわけではありません。
MathML は人間に可読でデバッグには非常に好都合ですが、よほど簡単な場合をのぞき、手入力するには冗長で間違いやすいものです。
その代わり、制作者は数式エディタや変換プログラム、そして他の専門的なソフトウェアツールを用いて MathML を生成することが予想されます。逆に、レンダラーによっては、たとえばカット & ペーストの操作によって、ウェブページに直接含まれている他の情報から MathML へと次から次へと変換するかもしれません。
As a consequence, raw MathML markup is not
primarily intended for direct use by authors. While MathML is
human-readable, which helps a lot in debugging it, in all but
the simplest cases it is too verbose and error-prone for hand
generation. Instead, it is anticipated that authors will use
equation editors, conversion programs, and other specialized
software tools to generate MathML. Alternatively, some
renderers and systems supporting mathematics may convert other
kinds of input directly included in Web pages into MathML on
the fly, in response to a cut-and-paste operation, for
example.
いくつかの面で、MathML は Adobe の PostScript のような他の低レベルなコミュニケーションフォーマットに類似しています。
PostScript ファイルは、必要に応じて様々な方法で作成することができます;エキスパートなら手入力で書いて調整し、物書きならワードプロセッサーで作成し、グラフィック・アーティストならイラストプログラムを使う、といったように。
しかし、プリンターや画面上のプレビューソフトといった PostScript の描画機器が広く普及しているので、一度 PostScript ファイルができあがってしまえば、非常に多くの大衆とそのファイルを共有することができます。
In some ways, MathML is analogous to other low-level,
communication formats such as Adobe's PostScript language. You
can create PostScript files in a variety of ways, depending on
your needs; experts write and modify them by hand, authors
create them with word processors, graphic artists with
illustration programs, and so on. Once you have a PostScript
file, however, you can share it with a very large audience,
since devices which render PostScript, such as printers and
screen previewers, are widely available.
MathML を、低レベルで汎用的なコミュニケーション層のためのマークアップ言語として設計する理由の一つは、上位の層における数学用のウェブ用ソフトウェアの開発を促進するためです。
MathML によって、モジュール構成の制作ツールや描画ソフトウェアの開発を統制する方法が提供されます。
MathML は、大きなシステム中の機能的な部品の開発を簡単にすることにより、決定的な量 のソフトウェア開発を促すことができ、その結果ウェブにおける数学の潜在的なユーザーが恩恵を受けることになるのです。
Part of the reason for designing MathML as a markup
language for a low-level, general, communication layer is to
stimulate mathematical Web software development in the layer
above. MathML provides a way of coordinating the development
of modular authoring tools and rendering software. By making
it easier to develop a functional piece of a larger system,
MathML can stimulate a `critical mass' of
software development, greatly to the benefit of potential
users of mathematics on the Web.
数学のデータに対しても、PosrScript と同様の状況を思い描くことができるでしょう。
制作者は、そのニーズに最適なツールを用いて自由に MathML 文書を作成することができます。
たとえば、学生なら XHTML ファイルに MathML を書き出すことができるメニュー方式の数式エディターをより好むでしょう。
研究者なら、自動的に式中の数学的な意味合いを符号化する数式処理パッケージを使うことによって、ウェブページから引用でき、同僚によって評価できることを望むでしょう。
学術機関誌の出版社なら、TEX のマークアップを HTML や MathML に変換するプログラムを好むでしょう。MathML を含むウェブページは作成時に用いられた方法に依らず、一度できあがってしまえば、強力で汎用的なコミュニケーション層のすべてのメリットが利用できるようになるのです。
様々な MathML ソフトウェアによって同じ一つの文書を、読み上げたり、印刷したり、数式処理システムに送ったり、あるいはウェブ文書の大きな集合の中の一部として扱うことができます。
MathML は符号化のプロセスで、数式を高い画質で印刷するために、業界で広く認知されている TEX をはじめとする標準的な植字や組版の言語に変換され直すでしょう。
最終的に、MathML がスプレッドシート、統計パッケージや技術ツールのような数学の方程式を生み出す他の舞台へ統合されることも期待できます。
One can envision a similar situation for mathematical data.
Authors are free to create MathML documents using the tools
best suited to their needs. For example, a student might
prefer to use a menu-driven equation editor that can write out
MathML to an XHTML file. A researcher might use a computer
algebra package that automatically encodes the mathematical
content of an expression, so that it can be cut from a Web
page and evaluated by a colleague. An academic journal
publisher might use a program that converts TEX markup to
HTML and MathML. Regardless of the method used to create a Web
page containing MathML, once it exists, all the advantages of
a powerful and general communication layer become available. A
variety of MathML software could all be used with the same
document to render it in speech or print, to send it to a
computer algebra system, or to manage it as part of a large
Web document collection. To render high-quality printed
mathematics the MathML encoding will often be converted back
to standard typesetting and composition languages, including
TEX which is widely appreciated for the job it does in this
regard. Finally, one may expect that eventually MathML will be
integrated into other arenas where mathematical formulas
occur, such as spreadsheets, statistical packages and
engineering tools.
W3C 数学ワークグループは、描画・作成ツールを含む、広範な MathML ソフトウェアがすぐに利用できるように、ベンダーに働きかけています。
現在の MathML ソフトウェアのリストは W3C 数学 の公開されたページ にて利用できます。
The W3C Math Working Group has been working with vendors to ensure
that a variety of MathML software will soon be available, including
both rendering and authoring tools. A current list of MathML software
is maintained on the public Math
page at the World Wide Web Consortium.
1.3.2 他のウェブ技術との関係
HTML Math の元来のコンセプトは、ブラウザーで直接的に実装されるという、単純かつ率直な HTML の拡張でした。
しかし、ウェブの爆発的な成長により、一般的な拡張のメカニズムが必要であること、そして数学は数ある構造化されたデータの一種に過ぎずそのメカニズムを利用してウェブに統合されなければならないことが、非常に早い段階から明らかになりました。
The original conception of an HTML Math was a simple,
straightforward extension to HTML that would be natively
implemented in browsers. However, very early on, the
explosive growth of the Web made it clear that a general
extension mechanism was required, and that mathematics was
only one of many kinds of structured data which would have to
be integrated into the Web using such a mechanism.
もしも MathML がウェブに拡張機能として統合される場合、MathML や MathML ソフトウェアは従来のウェブ環境とうまく相互作用できることがきわめて重要です。
特に、MathML は 3 通りの相互作用の方法を念頭に置いて設計されてきました。
まず第一に、数学を含むウェブコンテンツを作成するために、従来の言語を MathML に変換でき、制作ツールが MathML を生成できるように修正可能でなければなりません。
次に、将来のブラウザーやサーチエンジン、そして現在 HTML を扱うすべてのウェブアプリケーションが MathML のマークアップを HTML マークアップの中に継ぎ目なく埋め込むことが可能であることも必要です。
そして最後に、理想的ではないとしても、HTML 中に埋め込まれた MathML を既存のウェブブラウザーの中で何らかの方法で描画できることが必要です。
HTML が XHTML に変遷するにつれ、これらの事項はますます必要とされていきます。
Given that MathML must integrate into the Web as an
extension, it is extremely important that MathML, and MathML
software, can interact well with the existing Web environment.
In particular, MathML has been designed with three kinds of
interaction in mind. First, in order to create mathematical
Web content, it is important that existing mathematical markup
languages can be converted to MathML, and that existing
authoring tools can be modified to generate MathML. Second,
it must be possible to embed MathML markup seamlessly in HTML
markup, as it evolves, in such a way that it will be
accessible to future browsers, search engines, and all the
kinds of Web applications which now manipulate HTML. Finally,
it must be possible to render MathML embedded in HTML in
today's Web browsers in some fashion, even if it is less than
ideal. As HTML evolves into XHTML, all the preceding requirements
become increasingly needed.
ワールド・ワイド・ウェブは、今や完全に国際的に連携した動向です。
そして、数学は世界中で用いられている "ことば" です。
科学やエンジニアリングにおける数学の表記法は、その土地の自然言語を基盤として組み込まれています。
W3C は、世界中にコミュニケーションの可能性を広げるための建設的な勢力となれるよう努力しています。
従って、MathML も国際化の問題に遭遇するでしょう。
故意に左から右へかかれる言語との互換性をとったわけではありませんが、MathML 2 はデフォルトの記述方向は左から右へとなっていて、自然言語によっては埋め込まれた数式を記述するというニーズをまだ満たしていないのは明らかです。
いわゆる「双方向性」技術は未だ開発中であり、そういう意味では数式におけるサポートは将来の開発者の扱うべき問題になってしまうでしょう。
The World Wide Web is a fully international and
collaborative movement. Mathematics is a language used all
over the world. The mathematical notation in science
and engineering is embedded in a matrix of local natural
languages. The W3C strives to be a constructive force
in the spread of possibilities for communication throughout
the world. Therefore MathML will encounter problems
of internationalization. This version of MathML is
not knowingly incompatible with the needs of languages
which are written from left to right. However the
default orientation of MathML 2 is left-to-right, and
it is clear that the needs for the writing of
mathematical formulas embedded in some natural languages
may not yet be met. So-called bi-directional technology
is still in development, and better support for formulas
in that context must be a matter for future developers.
1.3.2.1 既存の数学マークアップ言語
おそらくここ 20 年間での数学マークアップ言語への最も重要な影響は、Donald Knuth によって開発された TEX 植字システムでしょう [Knuth1986]。
TEX は、数学の研究者の間では事実上の標準規格であり、そして科学の世界でも広く普及しています。TEX は、視覚的な描画の品質に対する標準を設定し、MathML が同等の視覚的な描画品質を提供できるようにするために多大な努力が費やされました。
そして、TEX の多くの遺産的な文書ゆえ、そして TEX に精通した多くの制作者のために、MathML の設計上の優先項目は、TEX の数学の入力を MathML に変換する能力でした。
そうした変換の能力は、プロトタイプのソフトウェアによって証明されたのでした。
Perhaps the most important influence on mathematical markup
languages of the last two decades is the TEX typesetting
system developed by Donald Knuth [Knuth1986].
TEX is a de facto standard in the mathematical research
community, and it is pervasive in the scientific community at
large. TEX sets a standard for quality of visual rendering,
and a great deal of effort has gone into ensuring MathML can
provide the same visual rendering quality. Moreover, because
of the many legacy documents in TEX, and because of the
large authoring community versed in TEX, a priority in the
design of MathML was the ability to convert TEX mathematics
input into MathML format. The feasibility of such conversion
has been demonstrated by prototype software.
数学を符号化するための大規模な作業は SGML の世界でも行われており、SGML に基づいた符号化方法は商業出版者に広く使われてきました。
ISO 12083 は、数学の表記法の視覚的な表現を記述するための DTD の断片を含む重要なマークアップ言語です。
ISO 12083 やその派生物による数学の表記法は、表現上多くの点で TEX と似ており、しかも SGML は TEX よりも構造や秩序を求めるので、MathML を TEX 互換にする作業は ISO 12083 に対しても行われました。
Extensive work on encoding mathematics has also been done
in the SGML community, and SGML-based encoding schemes are
widely used by commercial publishers. ISO 12083 is an
important markup language which contains a DTD fragment
primarily intended for describing the visual presentation of
mathematical notation. Because ISO 12083 mathematical notation
and its derivatives share many presentational aspects with
TEX, and because SGML enforces structure and regularity more
than TEX, much of the work in ensuring MathML is compatible
with TEX also applies well to ISO 12083.
MathML では、他の数学ソフトウェア、特に数式処理システムとの互換性の問題に特別な注意を払っています。多くの MathML のプレゼンテーション要素は、植字のボックス機構から派生している部分があります。
MathML のコンテンツ要素は、mathematical DTD fragment に関して OpenMath プロジェクトや Stilo Technologies 社の恩恵を多大に受けています。OpenMath プロジェクトは SGML と数式処理システムのコミュニティと非常に密接な関係があり、数学ソフトウェアパッケージとそれ以外のソフトウェアとの間での情報伝達の手段を SGML や XML 主体の方法を基本としています。
数式処理システムにおける MathML の生成や解釈の実行可能性は、すでにプロトタイプのソフトウェアによって実証されてもいます。
MathML also pays particular attention to compatibility with
other mathematical software, and in particular, with computer
algebra systems. Many of the presentation elements of MathML
are derived in part from the mechanism of typesetting
boxes. The MathML content elements are heavily indebted to the
OpenMath project and the work by Stilo Technologies on a
mathematical DTD fragment. The OpenMath project has close ties
to both the SGML and computer algebra communities, and has
laid a foundation for an SGML- and XML-based means of
communication between mathematical software packages, amongst
other things. The feasibility of both generating and
interpreting MathML in computer algebra systems has been
demonstrated by prototype software.
1.3.2.2 HTML の拡張機構
上で述べたように、HTML の成功により様々なデータタイプとソフトウェア・アプリケーションをウェブに取り入れることに莫大な圧力がかかるようになりました。
新しいフォーマットやアプリケーションは HTML やブラウザーベンダーに対して潜在的に新たな要求となります。
ここしばらく、新しい HTML の拡張を受け入れるためには、HTML の一般的な拡張機構が必要であることがわかってきました。
当初は、ワークグループでは HTML 3.2 において提案された数学を追加しようとした方法と同じような考えで、HTML そのものを単純に拡張することを考えていました。
しかし種々の理由により、詳細を考えるとこれはあまり賢い考えではないことがわかりました。
MathML の作業が始まって以来、そうした一般的な拡張機構として XML が主な候補として現れました [XML]。
As noted above, the success of HTML has led to enormous
pressure to incorporate a wide variety of data types and
software applications into the Web. Each new format or
application potentially places new demands on HTML and on
browser vendors. For some time, it has been clear that a
general extension mechanism is necessary to accommodate new
extensions to HTML. At the very beginning, the working group
began its work thinking of a plain extension to HTML in the
spirit of the first mathematics support suggested for HTML
3.2. But for a good number of reasons, once we got into the
details, this proved to be not so good an idea. Since work
first began on MathML, XML [XML],
has emerged as the dominant such
general extension mechanism.
XML とは、拡張可能なマークアップ言語 (eXtensible Markup Language) のことです。
XML は SGML の簡略版として設計された、HTML の文法や構文を定義するためのメタ言語です。
XML をウェブでの使用に適したものにし、今回の議論のようなときに HTML の一般的な拡張機構として用いることができることが XML の目標の一つです。
その名が示すとおり、拡張性こそが XML の一番の特徴です;制作者は自由に新しい要素や属性を宣言したり使用したりできます。
同時に、XML の文法や構文規則は文書構造に厳密さを求めるため、コンピュータによる処理や膨大量の文書の管理が容易になります。数学的にいうと、XML は元来 2 次元のツリー構造の表記法であり、従って符号化のツールとしてよい一般性をもっているのです。
XML stands for Extensible Markup Language. It is designed as a
simplified version of SGML, the meta-language used to define the
grammar and syntax of HTML. One of the goals of XML is to be suitable
for use on the Web, and in the context of this discussion it can be
viewed as the general mechanism for extending HTML. As its name
implies, extensibility is a key feature of XML; authors are free to
declare and use new elements and attributes. At the same time, XML
grammar and syntax rules carefully enforce regular document structure
to facilitate automatic processing and maintenance of large document
collections. Mathematically speaking XML is essentially a notation for
decorated rooted planar trees, and thus of great generality as an
encoding tool.
当初 W3C 数学ワークグループが立ち上がったときから、XML はブラウザーベンダーをはじめとする産業界の多大な支持を集めてきました。
W3C にとって HTML を XML の形に移行することは重要でしたので、モジュール化された新しい HTML の形式である XHTML の勧告という結果になりました。
MathML は、XHTML によくあう一つのモジュールとして考えることもできます。
実際、セクション A.2 [MathML as a DTD Module] では、W3C HTML ワークグループとの協力の下で生まれた新しい数学用の DTD が用意されています。
Since the setting up of the first W3C Math Working Group,
XML has garnered broad industry support, including that of
major browser vendors. The migration of HTML to an XML form
has been important to the W3C, and has resulted in the XHTML
Recommendation which delivers a new modularized form of HTML.
MathML can be viewed as another module which fits very well
with the new XHTML. Indeed in Section A.2 [MathML as a DTD Module]
there is a new DTD for mathematics which is the result of
collaboration with the W3C HTML Working Group.
さらに、すべての文書の公開方法や処理方法に対応した他の XML アプリケーションの保証が重要となっています。
必然的に、理論的で実用的な背景により、MathML を XML アプリケーションとしてとらえる方向性が生まれました。
Furthermore, other applications of XML for all kinds of
document publishing and processing promise to become
increasingly important. Consequently, both on theoretical and
pragmatic grounds, it has made a great deal of sense to
specify MathML as an XML application.
1.3.2.3 ブラウザーの拡張メカニズム
これまでに、MathML 1.0 勧告が採用されたときの状況とは異なり、HTML を拡張する XML の描画方法や処理方法の詳細がずいぶんと明確になってきました。
Cascading Style Sheets and Formatting Properties (CSS&FP) ワーキンググループによって開発された Formatting Properties (訳注: http://www.w3.org/Style/CSS/ あたりを読むと、そんなことが書いてあるようにも見えます) は文書オブジェクトモデル (DOM) を通じて利用できますが、MathML のプレゼンテーションにおいて、この Formatting Properties を利用することで MathML 要素の文体のコントロールが可能になります。
この Formatting Properties は、CSS&FP ワーキンググループと、XSLワーキンググループのが中心となって開発しています。
この話題に関する紹介は、第7章「MathML インターフェース」での議論をご覧下さい。
現在のシステムの下でどのように MathML を描画するかに関して詳細な注釈が W3C 数学ワーキンググループのホームページにあります。
By now, as opposed to the situation when the
MathML 1.0 Recommendation was adopted, the
details of a general model for rendering and processing XML
extensions to HTML are largely clear. Formatting Properties,
developed by the Cascading Style Sheets and Formatting
Properties Working Group for CSS and made available through
the Document Object Model (DOM), will be applied to MathML
elements to obtain stylistic control over the presentation of
MathML. Further development of these Formatting Properties
falls within the charters of both the CSS&FP and the XSL
working groups. For an introduction to this topic see the
discussion in Chapter 7 [The MathML Interface]. For detailed
commentary on how to render MathML with current systems
consult the
W3C Math WG Home Page.
スタイルシートのメカニズムを利用すれば、ブラウザーだけでMathMLのレンダリングを可能にすることもできます。
しかし、ウェブページに埋め込まれた要素によってブラウザーを拡張する必要性がなくなったわけではありません。
確かに特定のレンダラーを埋め込むことでブラウザーに MathML のような XML マークアップを処理できるようにさせるメカニズムもできあがっていますが、周りのウェブページにあわせて望み通りに表示させられるレベルには達していません。
この点については、第7章「MathMLのインターフェース」をご参照下さい。
Until style sheet mechanisms are capable of delivering
native browser rendering of MathML, however, it is necessary
to extend browser capabilities by using embedded elements to
render MathML. It is already possible to instruct a browser to
use a particular embedded renderer to process embedded XML
markup such as MathML, and to coordinate the resulting output
with the surrounding Web page, however the results are not yet
entirely as one wishes. See Chapter 7 [The MathML Interface].
数式処理システムへの接続のような特殊な処理を可能にするためには、他のプログラムへの出力の機能が強く望まれるでしょう。
しかし、実際に満足できるほどの相互作用のためには、ブラウザーと埋め込み要素との間の複雑な相互作用を可能にするのに十分な文書オブジェクトモデル (DOM) を定義しなければなりません。
この理由のために、W3C の数学ワークグループは、DOM ワークグループと密接に協力していくよう努力しています。
この成果は、第8章「MathML 用の 文書オブジェクトモデル」にて述べられています。
For specialized processing, such as connecting to a
computer algebra system, the capability of calling out to
other programs is likely to remain highly desirable. However,
for such an interaction to be really satisfactory, it is
necessary to define a document object model rich enough to
facilitate complicated interactions between browsers and
embedded elements. For this reason, the W3C Math Working Group
has coordinated its efforts closely with the Document Object
Model (DOM) Working Group. The results are described in
Chapter 8 [Document Object Model for MathML].
埋め込み要素によって処理したり、科学ソフトウェアとの相互のコミュニケーションを行うには、スタイルシートを基本としたレイアウトモデルは理想的とは言えません。
なぜなら、利点が少ない割には実装が大きな負荷となり得てしまったり、すぐに廃れてしまうかもしれないブラウザーとレンダラーの間の調整だけに時間をとられてしまう、という欠点が多いためです。
For processing by embedded elements, and for
inter-communication between scientific software generally, a
style sheet-based layout model is in some ways less than
ideal. It can impose an additional implementation burden in a
setting where it may offer few advantages, and it imposes
implementation requirements for coordination between browsers
and embedded renderers that will likely be unavailable in the
immediate future.
こうした事情を鑑み、MathML の仕様では、属性を基本としたレイアウトモデルを定義しました。
このモデルは、実装次第では、複雑な数式を高品質に描画する上で非常に効果的になることがわかっています。
MathML のプレゼンテーション属性は、できるだけ W3C の Formatting Properties を利用しています。また、MathML 要素が受け容れる class, style, ID の属性は、CSS スタイルシートとの併用を考慮しています。
ただし現時点では、MathML の描画エンジンで CSS の機構まで実装したものはほとんどありません。
For these reasons, the MathML specification defines an
attribute-based layout model, which has proven very effective
for high-quality rendering of complicated mathematical
expressions in several independent implementations. MathML
presentation attributes utilize W3C Formatting Properties
where possible. Also, MathML elements accept class, style and id attributes to facilitate their use with
CSS style sheets. However, at present, there are few settings
where CSS machinery is currently available to MathML
renderers.
CSS スタイルシートのメカニズムの利用に関しては、すでに述べました。最近では、XSL のメカニズムは XML 文書を効率よく変換し描画するために利用されるようになってきました。
実際、この MathML のW3C勧告の HTML バージョンをはじめとするすべての配布形態は、XML ソースを XSL 変換言語のツールを使って用意されたものです。
こうした流儀の開発が MathML でも利用できるようになれば、この開発スタイルは利用可能なレンダリング環境において MathML のスタイル制御の支配的な方法になることが予想されます。
The use of CSS style sheet mechanisms has been mentioned
above. The mechanisms of XSL have also recently become
available for the transformation of XML documents to effect
their rendering. Indeed the alternative forms of this present
recommendation, including the definitive public HTML version,
have been prepared from an underlying XML source using XSL
transformation language tools. As further developments in
this direction become available to MathML, it is anticipated
their use will become the dominant method of stylistic control
of MathML presentation meant for use in rendering environments
which support those mechanisms.
概要: 数学用マークアップ言語 (MathML) バージョン 2.0
次: 2 MathML の基礎
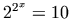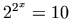 という数式について考えてみましょう。
この数式は、制作された環境 (周囲の文字が14ポイント) に合う大きさで作成されています。
当然、他の環境、つまり他のフォントの大きさでは、この数式は小さすぎたり大きすぎたりします。
次に気がつくのは、この数式の画像は白い背景に対して作られたということです。
従って、読み手やブラウザーがページの背景色を他の色に変えてしまうと、画像のアンチエイリアスの部分は白い「後光 (halo) 」になってしまいます。
という数式について考えてみましょう。
この数式は、制作された環境 (周囲の文字が14ポイント) に合う大きさで作成されています。
当然、他の環境、つまり他のフォントの大きさでは、この数式は小さすぎたり大きすぎたりします。
次に気がつくのは、この数式の画像は白い背景に対して作られたということです。
従って、読み手やブラウザーがページの背景色を他の色に変えてしまうと、画像のアンチエイリアスの部分は白い「後光 (halo) 」になってしまいます。
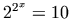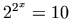 . This equation
is sized to match the surrounding line in 14pt type on the
system where it was authored. Of course, on other systems, or
for other font sizes, the equation is too small or too
large. A second point to observe is that the equation image
was generated against a white background. Thus, if a reader or
browser resets the page background to another color, the
anti-aliasing in the image results in white
`halos'.
. This equation
is sized to match the surrounding line in 14pt type on the
system where it was authored. Of course, on other systems, or
for other font sizes, the equation is too small or too
large. A second point to observe is that the equation image
was generated against a white background. Thus, if a reader or
browser resets the page background to another color, the
anti-aliasing in the image results in white
`halos'.
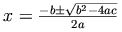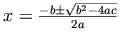 という数式を考えてみましょう。
これは周囲の文字の最上部よりも上に、水平の中心軸がある例です。
この数式には、ディセンダー
という数式を考えてみましょう。
これは周囲の文字の最上部よりも上に、水平の中心軸がある例です。
この数式には、ディセンダー 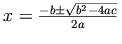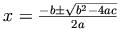 と配置することもできます。
こうすることにより、画像の中心線と数式の基準線が一致しますが、しかし行間隔の問題が発生し、結局数式が読みにくくなってしまいます。
さらに、画像の中心位置はブラウザーが異なれば処理のされ方も微妙に違うため、異なるクライアントに対して適切な位置関係を保証することが不可能になります。
と配置することもできます。
こうすることにより、画像の中心線と数式の基準線が一致しますが、しかし行間隔の問題が発生し、結局数式が読みにくくなってしまいます。
さらに、画像の中心位置はブラウザーが異なれば処理のされ方も微妙に違うため、異なるクライアントに対して適切な位置関係を保証することが不可能になります。