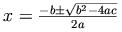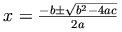1 はじめに

概要: 数学マークアップ言語(MathML) バージョン3.0
次: 2 MathMLの基礎

1 はじめに
    1.1 数学とその表記
    1.2 起源と目標
        1.2.1 MathMLの設計目標
    1.3 概要
    1.4 最初の例

1.1 数学とその表記

数学の特徴は、複雑かつ高度に発達した二次元の記号表記体系の利用でしょう。 J. R. Pierceがコミュニケーション理論に関する著書[Pierce1961]で記したように、数学とその表記は同一視するべきではありません。 数学的思想は、それを表現するための表記とは独立して存在することができます。 しかし、意味と表記との関係は微妙で、数学の持つ表現力や解析力の一部は記号的な形で思想を表現し操作できる能力に由来しています。 ウェブで数学を扱う上で、表記と内容（つまり意味）の両方をとらえ、高度に発達した印刷の表記上の慣例や電子メディアにおける相互接続性の可能性を文書から活用できるようにすることが、MathMLの誕生までの課題でした。

数学の表記は、思考の扱い表現する画期的な方法が発明され続けるのにともない、常に発達してきました。 今では一般的な代数学の表記ですら、それぞれの時代の最先端の数学者によって支持されながらも廃れてしまった多くのものを含め、驚くほど多様な形式を経てきました[Cajori1928]。 近代数学の表記は、改良の世紀の産物であり、高品質な活字のための表記の慣行は非常に複雑で繊細なものになってしまいました。 たとえば現在の一般的な活字では、数字を表す変数や文字は、通常の文章用のイタリック書体とは微妙に異なる数学用の特別なイタリック書体を用います（これはヨーロッパで16世紀後半に導入されたとみられます）。 ＋、ー、×、÷といった演算記号の周の前後の字間は、何世紀にもわたって改良されてきた演算子の優先順位に関する慣行を反映し、テキスト中のそれとは微妙に異なっています。 上付文字と下付文字の位置関係や括弧の大きさの選び方から数学の下位分野に特化された表記の慣例に至るまで、数学における活字の慣行だけのために何冊もの書籍が書かれてきました。 現在のデジタル活字・組版システムのニュアンスを表現するマニュアルは、数百ページに及ぶことさえあります。

数学や一般の印刷物における表記の慣行は、視線を導き、印刷された表現を読解しやすくします。 私たちは普段当たり前のように考えていますが、私たち近代の読者は、段落や大文字小文字、書体や書式、あるいはこの文書で用いられている節ごとに小数のような番号付けをする工夫にいたるまで、多くの慣行に依存しているのです。 そうした表記の慣行はおそらく、画面上で読む際の困難に妥協が求められる電子メディアにおいては、より一層重要になるでしょう。 コンピューターを考慮した適切な標準により、数学へのアクセスが印刷の世界を超えて広がるでしょう。 ウェブ以前に用いられていた数学のマークアップ手法の中には、TEX (TeXとも書かれます)[Knuth1986]やSGML([AAP-math]、[Poppelier1992]及び[ISO-12083])ベースの手法が広く知られています。

現在の数学表記の慣行の普及には目を見張るものがあります。 一般的な2次元のレイアウトや記号の多くは、近代の数学コミュニケーションでは、洋の東西を問わず見られます。 もちろん、記号の利用、特に関数や変数の命名に使われる記号は、ローカル言語や文字を反映していることもあるでしょう。 最も大きな違いは、一部のアラブ語圏では、数学表記全体を右から左へと、まるでヨーロッパの伝統を鏡に映したようにレイアウトするのです。

しかし、ウェブ上で数学を扱うということは、単にウェブブラウザーで伝統的な数学表記を表示する方法を見つける以上の意味があります。 ウェブは、知識の蓄積におけるメタファーの根本的な変化を象徴しており、そこでは相互接続性が中心的な役割を担っています。 自動処理、検索、索引付け、及び他の数学アプリケーションや文脈における再利用を可能にする数学のコミュニケーション方法を見つけることが重要になってきました。 このコミュニケーション技術の発展に伴い、数学の知見や理解を表現し、符号化し、そして究極的には他者と共有する機会があるのです。 私たちは、以下に仕様を策定するMathMLが、ウェブ上の数学の発展の重要な一歩であることを信じています。

1.2 起源と目標

1.2.1 MathMLの設計目標

MathMLは、当初より、以下に掲げる最終目標を念頭に設計されています。

MathMLは、理想的に、こうあるべき:

  • 数学の素材を、すべての教育及び科学コミュニケーションに適するよう符号化すること。

  • 数学の表記と意味の両方を符号化すること。

  • 表示の上でも意味の上でも、他の数学フォーマットとの間で変換が可能であること。出力フォーマットには、以下のものを含むべき:

    • グラフィカルな表示

    • 発声合成音声装置

    • コンピューター代数システムの入力

    • TEXのような他の数学組版言語

    • VT100エミュレーターのようなプレーンテキストの表示

    • 活字を含めた国際的な印刷メディア

    他の表記システムやメディアとの間の変換過程において、一部の情報が失われることは認識されています。

  • 特定のレンダラーやアプリケーションを意識した情報のやりとりを可能とすること。

  • 長い表現の効果的な閲覧を支援すること。

  • 拡張性を提供すること。

  • テンプレートその他の一般的な数式編集の技術によく適したものであること。

  • 人間に可読であり、ソフトウェアによる生成や処理が単純であること。

いかにMathMLがマークアップ言語としての目的を果たしたとしても、実装されなければ意味が無いことは明らかです。 W3C数学作業部会は、実装上の目標についても、以下の通り短いリストを作成しました。 これらの目標は、MathMLの描画・処理ソフトウェアが提供すべき最低限の機能について簡潔に述べるものです。

  • HTML及びXHTMLページ中におけるMathML式を、一般的なウェブブラウザーにおいて、読者及び作者の閲覧の好みに従い、プラットフォームの能力における高い品質で、適切に描画すること。

  • MathML式を含むHTML及びXHTML文書を、高品質なプリンター解像度で印刷すること。

  • ウェブページ中のMathML式が、マウスの動きのようなユーザーの動作に反応できること。また、ブラウザーを通して他のアプリケーションとコミュニケーションの調整ができること。

  • MathML式を含むウェブページの作成を容易にするような数式エディターやコンバーターが開発されるべきこと。

これらの目標がいかに達成されるかは、ブラウザーベンダーと他の開発者の協力と支援次第です。 W3C数学作業部会は、こうした科学コミュニティのニーズが満たされるよう、W3Cの他の作業部会やW3C外で働きかけてきました。 MathML 2とその実装は、MathML 1.0 勧告 (1998年4月) [MathML1] の際の状況から比べ、この分野において相当な進展を遂げました。 MathML3及び発展中のウェブには、より多くの目標を達成することが期待されています。

1.3 概要

MathMLは「XMLアプリケーション」として設計されており、つまり、数学を表現するのにXMLマークアップを用いることを意味します。 MathMLの特徴は、マークアップに2つの主系統があることです: プレゼンテーションマークアップは、第3章 プレゼンテーションマークアップで議論されるもので、数式の「表示」に用いられます。 コンテンツマークアップは、第4章 コンテンツマークアップで議論され、数学の「意味」を伝えるために用いられます。 コンテンツマークアップは特に詳しく仕様策定されています。 この仕様は、同じくXMLアプリケーションである、コンテンツディクショナリーと呼ばれる形式を用います。 この形式は OpenMath Society [OpenMath2004]によって開発されたもので、本仕様によって用いられるディクショナリーもOpenMath SocietyとW3C数学作業部会の共同開発により作成されました。

いずれの系統のマークアップにも共通する基礎は第2章 MathMLの基礎で取り扱っており、また、これらの系統を外部マークアップとともに組み合わせて単一のMathMLオブジェクトにする手法については 第5章 数式のマークアップ言語の混在 で議論しています。 MathMLがいかにアプリケーションと相互作用するかについては、第6章 ホスト環境との相互作用で取り上げています。 最後に、特別な記号の議論や文字、実体、書体に関する問題については、第7章 文字、実体及びフォントにあります。

1.4 最初の例

この二次元方程式の解の公式は、単純ながらもMathMLマークアップの教育的な例となります。

x = \frac{-b\pm\sqrt{b^2 - 4ac}}{2a}

MathMLは、この公式のマークアップに2通りの方法を提供します。 1つめは、数式の実際の見た目---記号の並べられた2次元のレイアウト---を重視するもので、その例は以下の通りです。 2つめは、数学上の意味を重視するもので、その例は1つめの例の後に示されています。 

<mrow>
  <mi>x</mi>
  <mo>=</mo>
  <mfrac>
    <mrow>
      <mrow>
        <mo>-</mo>
        <mi>b</mi>
      </mrow>
      <mo>&#xB1;<!--PLUS-MINUS SIGN--></mo>
      <msqrt>
        <mrow>
          <msup>
            <mi>b</mi>
            <mn>2</mn>
          </msup>
          <mo>-</mo>
          <mrow>
            <mn>4</mn>
            <mo>&#x2062;<!--INVISIBLE TIMES--></mo>
            <mi>a</mi>
            <mo>&#x2062;<!--INVISIBLE TIMES--></mo>
            <mi>c</mi>
          </mrow>
        </mrow>
      </msqrt>
    </mrow>
    <mrow>
      <mn>2</mn>
      <mo>&#x2062;<!--INVISIBLE TIMES--></mo>
      <mi>a</mi>
    </mrow>
  </mfrac>
</mrow>

ここで、この公式中の上付き文字 2 について考えてみましょう。 これは自乗という演算を表していますが、上付き文字自体の意味は文脈に依存しています。 上付き文字は、ベクトルの特定の成分を強調することもあれば、単なるラベルとして使われることもあるでしょう。 同様に、続けて書かれた2つの文字は、この公式で使われたように2つの変数の掛け算を意味したり、あるいは単一の変数の名前を表す2文字として使われることもあります。 多くの一般的な式の数学上の意味をより正確に特定できるものが、MathMLでコンテンツマークアップと呼ばれるものです。 このスタイルを用いると、2次元方程式の解の公式は、以下のようになります。 

<apply>
  <eq/>
  <ci>x</ci>
  <apply>
    <divide/>
    <apply>
      <plus/>
      <apply>
        <minus/>
        <ci>b</ci>
      </apply>
      <apply>
        <root/>
        <apply>
          <minus/>
          <apply>
            <power/>
            <ci>b</ci>
            <cn>2</cn>
          </apply>
          <apply>
            <times/>
            <cn>4</cn>
            <ci>a</ci>
            <ci>c</ci>
          </apply>
        </apply>
      </apply>
    </apply>
    <apply>
      <times/>
      <cn>2</cn>
      <ci>a</ci>
    </apply>
  </apply>
</apply>
概要: 数学マークアップ言語(MathML) バージョン3.0
次: 2 MathMLの基礎