[1] 時間的に角振動数 ω で振動する外力を加えた、減衰のある角振動数 ω₁ の調和振動子系を考える。運動方程式は、複素数の形式で書き直すと、次のように与えられる。

摩擦項のため、初期条件に依存する項は減衰するとして、強制振動の運動を と表す。

(a) = a / f₀ により複素応答関数 を定義するとき、 を ω の関数として求めよ。ここで は虚数部を表す。 (編注:もともとは ではなく Im でしたが、プラグインで表示できませんでした)

(b) が最大となる ω を求め、また の略グラフを書け（ω＞0の範囲でよい）。

[2] 中心力場 U(r) における質点の運動を考える。エネルギー E と、面積速度の２倍 h は運動の保存量であり、E₀, h₀ と表す。軌道平面内に極座標 ( r, θ) をとることにする。

(a)　運動が有界 (r_min ＜ r ＜ r_max) の場合、r が r_min から r_max まで増加し、再び減少して r_min に戻る間のθの増加分Δθは

dr

で与えられることを示せ。

(b) 中心力ポテンシャルが

で与えられるときに

の略グラフを書き、また運動する r の範囲、r_min と r_max を求めよ。ただし、エネルギーは運動ができる値を取るとする。

(c) (a)の結果を用いて、Δθを計算せよ。
ヒント :

,

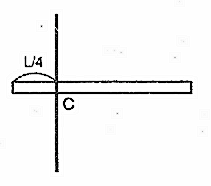
[3] 質量Ｍ, 長さＬの棒を考える。

(a) 棒の端から Ｌ／４ の点Ｃを通り棒に垂直な軸のまわりの慣性モーメントを計算せよ。

(b) 一般的に棒の端から の点を通り棒に垂直な軸のまわりの慣性モーメントはどうなるか。

[4] 一定の力 mg を受け手運動する質量 m の質点を考える。

(a) このときの質点の軌道は、 で記述されることを確かめよ。ただし、r₀, v₀ は時刻 0 における位置ベクトルと速度ベクトルである。

(b) ポテンシャルエネルギー Ｕ(r) を求めよ。

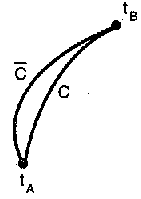
(c) Ｃと異なる仮想的な軌道 を考え、それは で記述されるとする。ただし、 の条件が課せられている。作用

に対して計算し、実際の軌道Ｃに対して作用が最小になることを示せ。ここでＴは運動エネルギーである。

　　注意：以下の事項を守らない場合、カンニングとみなされることがある。
※特に出題者からの許可がない限り、学生証、時計及び筆記用具以外のものを机の上に置かない。
　筆入れなども鞄等にしまい、鞄は机の中、脇の椅子または床の上に置く。
※教科書、参考書、ノート等は鞄等にしまう。
※解答用紙や計算用紙は所定の枚数以上に取らない。

wassy's workshop ( http://norihisa.washitake.com/ )